Démontrez que ce mouvement n'est pas perpétuel

[sitalgo]

Quand vous changez la hauteur de la masse, vous changez aussi la position du piston.

Bien sûr.

En vous n'avez pas le droit de faire la différence entre les deux énergies potentielles. Car ceci implique la conservation de l'énergie.
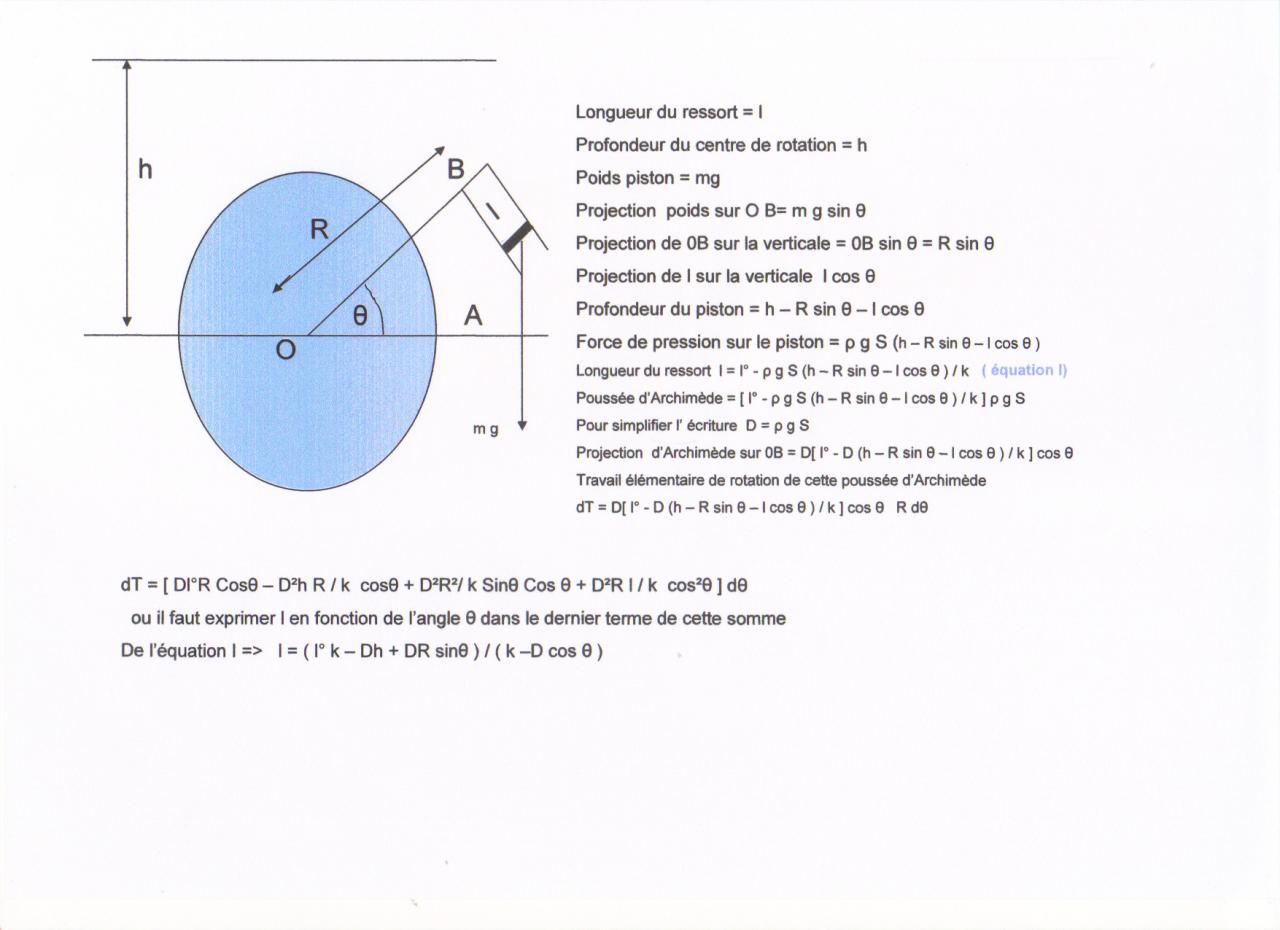
Il faudrait que vous calculiez le couple pendant la rotation du cylindre et le travail de ce couple.

Je fais le travail pour aller d'un point à un autre où seules comptent les forces verticales et qui ne dépendent pas du chemin parcouru.
Maintenant, que l'on refuse la conservation d'énergie sur un cycle complet, c'est normal, ça n'explique rien, mais sur des tronçons avec une force constante, ce serait miraculeux si le résultat était différent.
Cela dit, dans ma vision des choses le loup est ailleurs mais je n'arrive pas à mettre la main dessus.
-----

[sitalgo]

Les distances parcourrues sur la partie lineaire des masses des pistons ne sont peut être pas identiques...( à verifier )

Ca, c'est certain.

[stefjm]

Et je suis suffisamment mauvais en maths pour que l'affirmation que c'est une différentielle exacte me dise quelque chose.

M'enfin!
Depuis le temps qu'Amanuensis vous signale le truc!

C'est quand même des maths pour de la physique.
http://fr.wikipedia.org/wiki/Fonction_d'état

Je ne fais jamais un calcul si j'arrive à prouver qu'il sera nul avant de l'entreprendre. (Et avant de faire un calcul non nul, je fais toujours une AD pour avoir l'ordre de grandeur)
Question de réflexe de fisicien!

Du coup, je n'ai plus la moindre idée de ce que vous vouliez dire à propos du problème de calculer d(PV) au lieu de F.dx. Quand vous écrivez des m.g.dz, c'est bien aussi de l'énergie potentielle!

Bref, soit je comprends rien, soit je finis fou...Je vais faire du sport, histoire de varier les plaisirs.

Cordialement.

[invite15928b85]

Re.

Merci d'avoir l'indulgence d'oublier mon message #268 : erreur de calcul. dW n'est toujours pas une différentielle exacte. Dommage ...

Cordialement.

[invited729f73b]

Les frottements n’ont rien a voir ici, simplement parce qu'on peut toujours les rendre négligeables :

1) On peut toujours faire l’expérience dans un fluide très peu visqueux (air, voir helium 4)
2) On peut toujours faire l’expérience a vitesse très faible (Ce qui donnera Wf=>0)
cordialement,

Désolé Etorre mais je ne suis pas d'accord avec votre raisonnement qui à mon avis n'est valable que dans le cas ou ce que vous négligez, la force de Stokes, est obtenu en ne modifiant que très peu le phénomène que vous étudiez; dans votre raisonnement vous modifiez tout le phénomène ( plus de viscosité, vitesse très faible) pour négliger la force de Stokes, ce n'est pas un raisonnement valide !

Si votre raisonnement avait été appliqué par Millikan dans sa célèbre expérience, nous ne saurions toujours pas la valeur de la charge électrique de l'électron et toute notre réalité en aurait été changée;

Je crois que tous ces beaux calculs ne font que tourner en rond; d'autre part la force de Stokes n'est pas une force de frottement comme les autres car elle inclut un paramètre caractéristique de la forme de l'objet en mouvement et on ne peut jamais l'annuler comme les autres forces de frottement. Pour ma part, les enseignements que j'ai subi professaient de ne jamais la négliger dans les équations établissant la somme de forces en présence.

A mon avis, il n'est pas sage de n'en pas tenir compte dans ce dispositif car son influence agira bien avant la réalisation de la possibilité du retournement des godets et aura absorbé tout le travail produit par la force d'Archimède sans l'aide du moindre piston;

La seule condition pour démontrer que ce dispositif n'est pas perpétuel consiste, une fois ayant reconnue la relation qui existe entre un coefficient de frottement d'un arbre de rotation d'une poulie et son impédance donc aussi le travail fourni par la force et la différence de potentiel durant le temps de l'expérience, à constater que le coefficient de frottement de l'arbre ne varie pas au cours du temps en diminuant, c'est à dire qu'il n'existe pas de source de variation de travail interne au système Poulie courroie godet à piston et de procéder ainsi pour tous les coefficients de frottements: si tous les coefficients de frottements, sont constants au cours du temps, le dispositif ne peut etre perpétuel car il ne peut exister ainsi une ou plusieurs sources de variation de travail interne et pas d'énergies potentielles internes qui apparaitraient de ce fait !

Bien sur, vous faites ce que vous voulez, mais je pense que çà vaut mieux que de tourner en rond !

Au revoir...

[Amanuensis]

Merci d'avoir l'indulgence d'oublier mon message #268 : erreur de calcul. dW n'est toujours pas une différentielle exacte. Dommage ...

Votre démarche dans le #268 est correcte, et doit aboutir à la conclusion que c'est une dérivée exacte. (Et il n'y a même pas besoin de calculer les différentielles secondes croisées, l'écriture sous la forme est facile à obtenir en définissant comme il faut les fonction z_m, z_a et V (trois fonctions de z et \theta), resp. profondeur du centre de gravité de m, pression à la profondeur du centre géométrique du volume de vide, et le volume du volume de vide.)

Par exemple = dans les parties verticales et = dans les retournements (avec un h différent en haut et en bas). Le test si on est dans une partie verticale ou un retournement, et lequel, se fait sur z et \theta.

Avec une telle définition conditionnelle des fonctions, la formule ci-dessus pour dW s'applique pour toutes les phases.

Pour les signes des formule en z et \theta, faudrait choisir une bonne fois pour toute si z représente une hauteur ou une profondeur.

[invite15928b85]

Bonjour.


Amanuensis, le fait est que la différentielle que je calcule n'est pas une différentielle totale exacte.


Cela dit, j'envisage une autre approche : enfermer une machine de Calculair dans une enceinte déformable parfaitement souple et faire tourner la machine via un axe solidaire d'une des poulies et qui traverse l'enveloppe. Au cours d'un cycle, le volume interne de l'enceinte variant, il y a échange de travail avec le milieu extérieur via la paroi de l'enceinte. Le bilan du travail globalement échangé avec le milieu extérieur, par l'axe et par la paroi de l'enceinte, doit être nul cette fois, si j'ai bien tout compris.


@+

[calculair]

Bonjour à Tous,

Je me suis interessé tout particulièremement à la phase de rotation, dont je vous livre ma reflexion

Le rayon de rotatopn est R
la longueur au repos du ressort de coefficient k, est l° et le piston est vide d'air

Pour simplifier l'ecriture le terme Rho g S = D , ou S est la surface du piston

J'espère avoir eté assez clair pour qu'il soit facile de verifier les expressions....

merci à tous...

[invite6dffde4c]

Bonjour.


Amanuensis, le fait est que la différentielle que je calcule n'est pas une différentielle totale exacte.


Cela dit, j'envisage une autre approche : enfermer une machine de Calculair dans une enceinte déformable parfaitement souple et faire tourner la machine via un axe solidaire d'une des poulies et qui traverse l'enveloppe. Au cours d'un cycle, le volume interne de l'enceinte variant, il y a échange de travail avec le milieu extérieur via la paroi de l'enceinte. Le bilan du travail globalement échangé avec le milieu extérieur, par l'axe et par la paroi de l'enceinte, doit être nul cette fois, si j'ai bien tout compris.


@+

Bonjour.
Je suis d'accord avec vous à propos de la différentielle exacte. Surtout que la fonction "d'état" n'a qu'un seul degré de liberté et que ce n'est pas un système thermodynamique mais purement mécanique.

Mais je ne suis pas d'accord avec votre proposition. Le but n'est pas de démontrer que le dispositif ne fonctionne pas comme un mobile perpétuel. Ça, on le sait déjà.
Le but est de faire la démonstration "à la dure" en calculant le travail fait en un tour par un godet en intégrant F.dx. Les méthodes "globales" reviennent à utiliser la conservation de l'énergie: la force dérive d'un potentiel

Donc il faut écrire la valeur de F.dx, comme j'ai fait, mais sans faire des erreurs, comme ceux que j'ai évidemment faits.
Chanur, Amanuensis et vous même avez trouvé quelques-uns. Il faut trouver les autres.
Cordialement,

[invite6dffde4c]

Bonjour à Tous,

Je me suis interessé tout particulièremement à la phase de rotation, dont je vous livre ma reflexion
...

Bonjour Calculair.
Il y a une erreur de signe da la profondeur du piston: h - r sin(th) + l cos(th)
La projection des forces sur OB n'est pas intéressante. OB est fixe. C'est sur la perpendiculaire à OB qu'il faut travailler. Ces sont ces forces qui travaillent.
Et quand vous calculez le travail, il faut tenir compte que la poussée d'Archimède a sont centre de poussée au milieu du vide (donc, à l/2). Vous pouvez calculer le travail en calculant le couple de la force d'Archimède el la multipliant par son bras de levier: {r.cos(the) + (l/2)sin(the)} Mais il ne fit pas oublier le travail couple du poids mg: avec un bras de levier différent: {r.cos(the) + l.sin(the)} et de direction opposée.

Si vous regardez mes calculs et corrigez la dernière erreur trouvée par Fanch5629:


Vous constaterez que c'est la même chose que vous avez faite, avez des erreurs déjà corrigées (nous avons un peu d'avance).

Le problème est qu'il en reste encore des erreurs et que je ne les vois pas. Ça peut être des erreurs bêtes (et toujours gênantes) de signe, ou des erreurs de fond ou de modélisation.
Cordialement,

[Amanuensis]

Amanuensis, le fait est que la différentielle que je calcule n'est pas une différentielle totale exacte.

C'est alors parce que la forme différentielle dont vous partez n'est pas celle de de l'énergie. Genre il y a une faute de signe dedans.

Quelle est-celle cette forme en question ?

[calculair]

bonjour LPFR,

Merci d'avoir regardé mon calcul, je vais reprendre cela à la lumière de vos reflexions dans l'aprés midi.

Bien cordialement et à tout à l'heure avec une version corrigée

[Amanuensis]

Sinon, non, les formules dont on parle n'ont pas qu'un degré de liberté, mais deux : z et \theta (pour un godet, et 2n s'il y a n godets...). Le simple fait de calculer des trucs fois dz et d'autres fois d\theta montre que l'espace de travail est 2D, et alors tout le formalisme sur les formes s'appliquent. Qu'on puisse découper en phases dans lesquelles un seul degré joue ne change rien (et est une perte de généralité, la méthode par formes différentielles marcherait si la courroie faisait un trajet quelconque et que les godets changeaient d'orientation n'importe comment).

Ce formalisme, et les maths correspondantes, n'ont rien de spécifique aux systèmes où les échanges de chaleur ou les échanges de matière interviennent. Il s'applique tout autant à un système mécanique dans lequel on écrit des différentielles.

C'est LPFR qui a introduit des calculs différentiels avec des dT, dz, d\theta. Affirmer maintenant que ce formalisme ne s'applique pas est une totale contradiction (et de toutes manières incorrect).

Quand aux erreurs, à partir du moment où on peut écrire

dW = mgdz_m-p_adV-Vdp_a

pour des fonctions (de z et \theta, les variables d'états) z_m, z_a et V,

l'intégrale sur un cycle est nulle.

Cela se vérifie par de simples groupements de termes, ainsi que des vérifications de continuité des formules aux transitions entre phase.

Par ailleurs certaines erreurs n'ont pas d'influence sur le résultat de l'intégration. Par exemple une écriture erronée de z_a (si elle reste continue et différentiable par morceaux) ne changera pas le résultat de l'intégrale. Même chose pour la formule donnant \ell en fonction de z et \theta...

[invite1c6b0acc]

Bonjour à tous
Je voudrais m'excuser de mon silence, mais je ne suis pas chez moi, je n'ai pas de compilateur, et comme ça fait plus de 25 ans que je n'ai pas fait de mécanique théorique j'ai trop peur de dire des bêtises...
Néanmoins, il me semble,effectivement, que le "loup" est d'avoir négligé le déplacement de l'eau.
@MarioB : même si la force de Stockes n'est pas négligeable pour un mécanisme réel, en tout état de cause elle ne peut que dissiper de l'énergie, et je crois que la machine ne peut pas fonctionner, même en supposant arbitrairement toutes les dissipations nulles. Peu importe que ce soit ou pas réaliste (on ne pourrait pas négliger ces forces pour calculer la vitesse d'ascension d'une montgolfière, mais on n'en a pas besoin pour prouver qu'une montgolfière monte).
@LPFR : Dans le cas général la conservation de l'énergie est un principe indémontrable, mais dans des cas particuliers (forces à flux conservatif), je crois qu'elle peut se démontrer purement mathématiquement.

Courage, on y arrivera !

[calculair]

Bonjour à tous , bonjour LPFR.


Voici une version corrigée grace aux remarques de LPFR et Fanch5629.

J'ai toujours un doute.

Pour ce qui concerne le travail du couple, je pense que l'on de fait pas d'erreur si on considère que les forces travaillent au niveau du bras de levier OB. C'est sur ce bras de levier qu'elles poussent la fameuse machine.


Si la formule est juste, il restera a calculer le travail pour un 1/2 tour à la pronfondeur h pour le centre de rotation et un autre 1/2 tour, toujours dans le meme sens à une profondeur h + X

[invite15928b85]

Re. et bonjour si ce n'est pas déjà dit.


A mon sens, la démonstration du non fonctionnement de la machine n'a pas encore été fait ici. Je suis d'ailleurs de plus en plus persuadé que raisonner sur un système ouvert est voué à l'échec. Mais je n'ai pas d'explication claire à donner : trop nul.


Cependant, je vous propose la manip suivante :


On prend une machine de Calculair monocylindre à ressort (pour faire simple) que l'on place dans une enceinte fermée et rigide remplie du même fluide qu'à l'extérieur.


Cette enceinte est équipée d'un tuyau de communication avec l'extérieur dans lequel coulisse librement et sans frottement un piston. Le tuyau est horizontal pour ne pas faire travailler le poids de ce piston. Dans ces conditions, les conditions d'environnement de la machine sont exactement identiques à celles qui seraient si l'enceinte n'existait pas : même pression au niveau du piston, même gradient de pression.


La différence est que, maintenant, on a affaire à un système fermé (ie qui n'échange pas de matière avec l'extérieur, mais qui peut échanger du travail avec l'extérieur via le piston, travail que l'on peut quantifier par le déplacement du piston).


Dans ces conditions, quand la machine réalise un cycle, l'observateur extérieur voit le piston aller et venir et retrouver sa position initiale quand le cycle est terminé, tout cela contre les forces de pression extérieures qui s'éxercent sur le dit piston. Sa conclusion est que, sur un cycle, la machine n'échange pas de travail avec l'extérieur. En particulier, elle n'en fournit pas.


Notre tors, à mon sens, est de persister à raisonner sur un système ouvert alors que la fermeture du système permet de conclure immédiatement.


Alors, comment faut-il poser le problème pour un système ouvert, je laisse la réponse à d'autres. Moi, je cale.


Cordialement.

[calculair]

Bonjour Fanch5629

Si nous demontrons que ma super machine tourne, au lieu de recuperer l'energie supplementaire au niveau des axes des poulies, nous la recupererions au niveau de ton piston....

Je pense que si malgres tout nos efforts nous concluons à un travail positif de cette machine, il ne restera plus qu'a faire la manip en vrai grandeur et la proposer aux ecologistes comme syteme à 0 emission de CO²....!!!

[invite6dffde4c]

Re-bonjour Calculair.
Vous êtes en train de refaire la même démarche que j'avais faite. Et que j'ai abandonnée.
Regardez ce qui arrive quand thêta = 90°. La poussée d'Archimède est verticale et sa projection sur la perpendiculaire à OB est nulle. Mais le couple du godet n'est pas nul. La poussée d'Archimède et le poids ont un bras de levier non nul par rapport à l'axe de rotation de la poulie. 'l/2' pour Archimède et 'l' pour le poids.
C'est pour cela que j'ai changé mon fusil d'épaule et je calcule maintenant le travail vertical d'Archimède et du poids. Ça complique un peu les formules, mais ça diminue le risque d'erreur.
Mais pas assez, puisqu'il en reste encore.
Si vous voulez utiliser le couple. Il faut tenir compte que ce centre de poussée d'Archimède se trous à l/2 de la culasse et que celui du poids se trouve à 'l' de la culasse. Puis il faut calculer le bras de levier pour chacun.
Cordialement.

[invite6dffde4c]

Bonjour Fanch5629

Si nous demontrons que ma super machine tourne, au lieu de recuperer l'energie supplementaire au niveau des axes des poulies, nous la recupererions au niveau de ton piston....

Je pense que si malgres tout nos efforts nous concluons à un travail positif de cette machine, il ne restera plus qu'a faire la manip en vrai grandeur et la proposer aux ecologistes comme syteme à 0 emission de CO²....!!!

Re.
Vous ne devriez pas faire des réponses comme ça. Elles risquent d'être mal interprétées (au premier degré).
Il est évident que la machine n'est pas un mobile perpétuel même si mes calculs (pourris) disent le contraire.
Cordialement,

[invite15928b85]

Re.

LPFR, je n'ai toujours pas compris vous persistez à calculer le travail du poids du piston. Les lois de Newton nous disent que ce poids ne travaille pas quand le CG décrit une trajectoire fermée dans un champ de pesanteur dérivant d'un potentiel, et cela sans faire appel à un quelconque principe de conservation de l'énergie.

Me trompé-je ?

Sinon pas de soucis pour la réponse de Calculair dont la postérité retiendra qu'il a inventé la fameuse "Machine de Calculair".

[invite6dffde4c]

Re.

LPFR, je n'ai toujours pas compris vous persistez à calculer le travail du poids du piston. Les lois de Newton nous disent que ce poids ne travaille pas quand le CG décrit une trajectoire fermée dans un champ de pesanteur dérivant d'un potentiel, et cela sans faire appel à un quelconque principe de conservation de l'énergie.

Me trompé-je ?

Sinon pas de soucis pour la réponse de Calculair dont la postérité retiendra qu'il a inventé la fameuse "Machine de Calculair".

Re.
J'ai déjà dit que je voulais calculer le travail d'un tour "à la dure". Et voir comment évolue le travail dans les virages (avec le poids du piston) permettra de bien voir comment se passent les choses. Notamment l'asymétrie entre les deux virages qui doit compenser l'asymétrie entre les deux parcours verticaux.
Très bon la "Machine à Calculair".
Cordialement,

[invited729f73b]

Bonjour,

je crois que j'ai trouvé une partie de ce qui a été peut-etre oublié: dans la partie descendante du mouvement des godets, le poids sur la membrane doit subir, du fait du mouvement dans le champ de gravitation du dispositif global, l'effet du principe d'équivalence et la valeur de son poids résultant est donc beaucoup plus faible, ce qui fait que son action sur la membrane est beaucoup moins creusante et le volume du godet ne varie donc pas autant qu'il y parait;

Il en résulte que la force d'Archimède dans la partie descendante est beaucoup plus proche de sa valeur dans la partie ascendante et la somme des travaux vont tendre à s'annuler bien avant un cycle !

Peut-etre une idée à creuser, à vos calculettes...

Au revoir...

[invite15928b85]

J'ai écrit "Machine de Calculair". Cette fois c'est vous, LPFR, qui écrivez des choses qui risquent d'être mal interprétées

[calculair]

bonjour LPFR

Ta remarque sur le couple " residuel" pour theta = 90° montre qu'effectivement, il faut considerer le centre de poussée et le centre de gravité pour calculer le travail du poids.

Je comprend que tu souhaites tres fort que cette machine ne puisse tourner. Moi aussi cela me rassurerai.....

Le travail durant la rotation superieure ne depend pas de la longueur de la machine ( longueur des parties lineaires plongeant dans l'eau )

Le travail dans la rotation inferieure risque d'être egal à celle de la partie superieure, puisque les ecarts de pression dans une rotation de même rayon sont les mêmes ( on pourrait changer les rayons des poulies pour complquer...)

Le travail sur les parties lineaires me semble positif. En effet on sait quand un sous marin commence à remonter, il remonte de plus en plus vite et si il est parfaitement equilibré, s'il commence à descendre il descendra de plus en plus vite, du fait des forces de pression et de l'elasticité de la coque.


Mille excuses d'embrouiller les choses, mais c'est pour montrer qu'il faut faire vraiment le calcul et je sais que tu es convaincu de la chose.

[invite15928b85]

Bonjour à tous.

C'est bien calme ici, ce matin ... le changement d'heure ?

Il y deux manifestations du travail des forces de pression à considérer :

1 - le travail de la poussée d'Archimède quand un cylindre se déplace (forme dW1 = V.dP), moteur de la machine,

2 - le travail lié à la variation de volume du cylindre qui aspire et refoule du fluide (forme dW2 = P.dV), influence sur le fluide environnant.

En fait, aucune des formes différentielles dW1 et dW2 n'est une différentielle totale exacte. Seule dW = dW1 + dW2 l'est. C'est ce qu'Amanuensis cherchait à nous expliquer, je crois.

Sur un cycle, W est nul (propriété des formes différentielles exactes, c'est des math, pas de la conservation d'énergie), W2 l'est aussi (voir la boite à piston d'hier).

Donc W1 l'est aussi car 0 - 0 = 0 (trop fort !)

Cela dit, il n'est pas interdit de vouloir calculer W1 directement sur un cas particulier, mais la conclusion n'aura aucun caractère de généralité.

Cordialement.

[Amanuensis]

Juste un point de notation : il est d'usage d'écrire pour une forme qui n'est pas en toute certitude exacte, et de noter avec un "d" seulement les formes exactes.

Ensuite le travail de la pression est donné traditionnellement avec le signe - : , c'est le travail reçu par le système dont le volume varie (travail négatif si le volume augmente, car cela se fait contre la pression).

De même le travail de la poussée d'Archimède à volume constant s'écrit avec un signe - : , car la force est dirigée dans le sens inverse du gradient de pression.

[calculair]

Bonjour tout le monde,

Le coup de la differentielle totale exacte, il faut me l'a detailler. Mes cours sont un peu loin et je n'ai pas suivi malheureusement toute la discussion.

Je ne sais qui avait montré que le système avait n points d'equilibre ( n = nb de godets). cela me semble plausible evidemment.

LPFR , comme moi souhaiteriont faire le calcul " à la dure" et je le comprend, car tous les raisonnements simplistes sont contre intuitifs ( voir mon message d'hier à 18H 21 ).

Je comprend que l'on souhaite trouver que cette machine ne tourne pas et ce type solution rassure.... Dans un cas litigieux, difficile, ou un "micro nano pico doute" peu s'installer, il est sage de faire le calcul complet ( avant de se lancer dans une manip, moins chère que celle de l'accelerateur de Genève pour montrer l'impossible aller plus vite que la lumière et je crois que cela se discute encore).....

[Amanuensis]

Au cas où cela aide :

En termes simplifiés une forme différentielle est exacte quand c'est le "gradient" (la différentielle, le "grad") de quelque chose.

Le cadre mathématique est la géométrie différentielle. Si un système est entièrement décrit à un instant donné par n variables d'état, l'état peut être vu comme un point d'une variété (différentielle) de dimension n. L'évolution du système est alors une "ligne" paramétrée par le temps dans cet espace d'état.

On peut alors parler d'espaces vectoriels tangent et cotangent en chaque point. L'espace vectoriel cotangent en un point est, d'une certaine manière celui des valeurs locales des "gradients" de fonctions d'état (de champs scalaires). Si est un système de coordonnées (local) de la variété, les différentielles locales des , notés , engendrent l'espace cotangent local. Toute combinaison linéaire , les étant des fonctions d'état différentiables (par morceaux), est un champ de formes (une 1-forme, une forme différentielle), mais n'est pas nécessairement un "gradient". On parle de forme exacte si ce champ l'est.

La notation "d" représente la dérivée extérieure (disons une dérivation anti-symétrisée). "d" appliquée à un champ scalaire f (une 0-forme ; en physique une fonction d'état) en donne le "gradient" (une 1-forme), c'est la différentielle de la fonction d'état , mais "d" s'applique à toute n-forme pour donner une (n+1)-forme. On a toujours , F étant une n-forme. Une forme est dite fermée si , ce qui correspond au test sur les différentielles croisées. Comme dd=0, une forme exacte est toujours fermée (mais l'inverse ne s'applique que sous certaines conditions topologiques).

L'intégrale d'une forme exacte, d'un "gradient" sur une ligne ne dépend que des extrémités et est simplement la différence de la valeur de la fonction d'état correspondante aux extrémités : , et donc l'intégrale d'un "gradient" est nulle sur un trajet fermé.

(1) Entre guillemets parce que le terme gradient est normalement utilisé pour un élément du tangent, celui obtenu en appliquant une métrique à la forme obtenue en différenciant une fonction d'état. En thermodynamique il n'y a pas de métrique, on distingue vecteurs et formes, et on travaille avec des différentielles de fonctions, pas avec les gradients correspondant.

(2) groupe d'homotopie trivial par exemple... Par exemple dans C* vu avec les coordonnées polaires (r,\theta), l'intégrale de sur un cercle entourant l'origine est 2\pi, non nulle. est fermée mais non exacte. Point d'ailleurs qu'en toute rigueur il faudrait prendre en compte dans le traitement discuté dans ce fil.

[invite15928b85]

Le tout dernier point doit pouvoir être contourné en considérant cos theta en lieu et place de theta comme variable d'état, non ?

[invite6dffde4c]

...

Cela dit, il n'est pas interdit de vouloir calculer W1 directement sur un cas particulier, mais la conclusion n'aura aucun caractère de généralité.

Cordialement.

Bonjour Fanch5629.
Nous savons que le résultat de l'intégrale est zéro. Soit par la conservation de l'énergie soit par les propriétés mathématiques des "choses". Ce résultat doit pouvoir être retrouvé par intégration analytique ou numérique.

Donc, je voudrais vous demander ce qu'il faut que je mette comme fonction à intégrer dans les quatre morceaux de mon intégrale de ligne. Les deux verticales où la variable est la profondeur et l'angle ne varie pas, et les virages où la profondeur et l'angle sont directement reliés. Car c'est sûrement là où se trouvent mes erreurs. Merci.
Au revoir.