re bonjour
Pour les adeptes des mouvements produisant de l'energie avec rien....
Le dispositif est une courroie qui passe sur les 2 poulies , les reservoirs sont fermes par une membrane elastique avec un poids
-----

re bonjour
Pour les adeptes des mouvements produisant de l'energie avec rien....
Le dispositif est une courroie qui passe sur les 2 poulies , les reservoirs sont fermes par une membrane elastique avec un poids
En science " Toute proposition est approximativement vraie " ( Pascal Engel)

bonjour à tous et bonjour phys4
Excusez moi pour mes mediocres dispositions en dessin. J'ai pris en compte les remarques de phys4 qui permettent une modelisation plus facile.
Je propose le schema ci joint, or on prend la precaution d'augmenter la distance entre les 2 poulies et on ajoute un grand nombre de cylindre de façon a pouvoir compenser le travail aux extremites qui reste sensiblement constant.
Ceci est je pense une amelioration utile....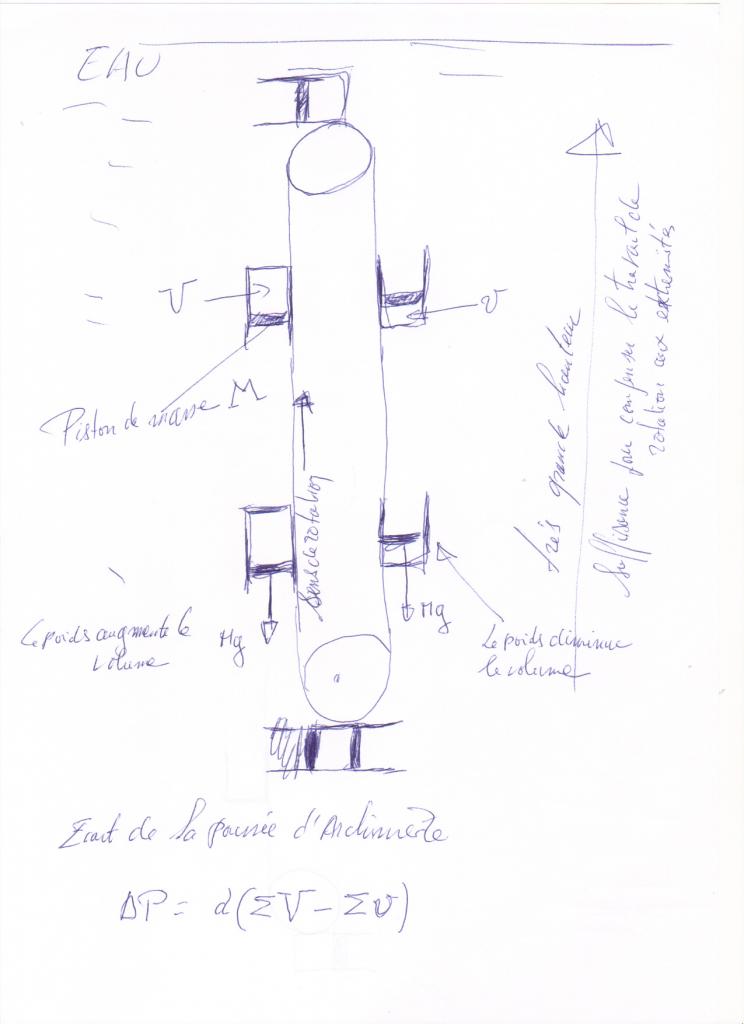
En science " Toute proposition est approximativement vraie " ( Pascal Engel)

Merci pour l'amélioration qui ne demande pas une nouvelle démonstration :
Explication, il faut des masse proportionnelles à la profondeur car si la pression hydrostatique devient trop forte les pistons sont repoussés et ils n'interviennent pas dans la poussée. Il y a donc un rapport de proportionnalité entre masse des pistons et profondeur utile
Donc les masses des pistons doivent effectuer le travail nécessaire pour vides les cylindres en positions basse. Ce travail est à fournir lors du basculement autour des poulies.
Le travail au extrémités est constant par cylindre, donc il se multiplie par la densité des cylindres également.Je propose le schéma ci joint, or on prend la précaution d'augmenter la distance entre les 2 poulies et on ajoute un grand nombre de cylindre de façon a pouvoir compenser le travail aux extrémités qui reste sensiblement constant.
Comprendre c'est être capable de faire.

Bonjour,
Le travail du poids sur la poulie basse est compensé par le travail du poids de la poulie haute.
En science " Toute proposition est approximativement vraie " ( Pascal Engel)

Pas exactement, c'est ce qui fait toute la différence, les poids arrivent en retard sur la poulie haute et il y a plus de poids sur la partie montante que la partie descendante.
A ce sujet il faut remarquer que le travail pour vider les cylindres n'est pas toujours situer sur la poulie basse.
Avec un dispositif descendant à grande profondeur, les cylindres sont écrasés par la pression, ce qui limite la partie utile à la hauteur permettant aux cylindres de se dilater (message précédent où j'indique une profondeur limite fonction de la masse). Lors de la remontée la pression permet au piston de descendre pour vider le cylindre, ce travail du piston est perdu pour le travail récupéré à la remontée.
Comprendre c'est être capable de faire.

Bonjour,
Avant de partir, je vous propose ce debut de calcul.
Je propose de calculer le travail fourni par le cylindre sur un tour complet. Le travail total que peut fournir le dispositif est la somme des travaux de chaque cylindre......S'il est positif c'est " EUREKA !!!!"
Ne nous excitons pas trop..
A la montée il faut ecrire au denominateur (P°Sh - mgh°)
Dernière modification par calculair ; 18/10/2011 à 08h39.
En science " Toute proposition est approximativement vraie " ( Pascal Engel)


Bonjour.
Je suis d'accord avec ce qui a été mentionne plus haut.
Pour démontrer qu'un "mobile perpétuel" ne fonctionne pas, il faut démontrer que les couples de forces qui le font tourner sont en équilibre.
Soit dans n'importe quelle position, soit dans celle d'équilibre stable (comme une roue avec le centre de masses décentrée).
Les arguments de travail ne sont pas recevables (du moins celui que les travaux sont les mêmes), puisque on part de ce que l'on veut démontrer. Il faut démontrer que le travail de chaque force se compense avec celui des autres.
Je ne me suis penché sur le mobile de Calculair (que je ne connaissais pas (le mobile, pas Calculair que je salue)) et je n'ai pas la démonstration, mais mon "pif" me suggère que tout se passe pendant le retournement. Et non dans la seule position extrême, mais pendant tout le basculement des cylindres.
Au revoir.

bonjour LPFR,
Ton pif est sans doute bon.
J'avais deja montré que si le dispositif est une immense roue, pour tourner, il faut lui injecter de l'energie.
Pour minimiser ce qui se passe dans la rotation aux extremités, j'ai proposé d'allonger la partie lineaire du système.... excuses moi si je complique un peu et cela tendance a noyer peut être le poisson....
En tous les cas il faut bien s'assurer que si le travail de rotation est constant, on ne peut le compenser par le travail moteur des parties lineaires
En science " Toute proposition est approximativement vraie " ( Pascal Engel)

Bonjour.
Ma modeste contribution à l'analyse du mobile de Calculair :
Si les évolutions du système sont suffisamment lentes, on peut les considérer comme réversibles au sens thermodynamique du terme.
Si l'on considère des transformations isothermes, par exemple, tous les points représentatifs de l'état du gaz du cylindre dans un diagramme P-V sont sur la même isotherme.
Le cycle de Carnot est de surface nulle : le bilan mécanique est nul.
Il est bien évident que les retournements du cylindre sont à prendre en considérations puisqu'il y a travail du piston contre les forces de pressions.
Dans le cas de transformations réelles, non réversibles, ce bilan est négatif. Lancé par apport d'énergie extérieure, il finit pas s'arrêter.
Cordialement.

Bonjour,
Je ne me suis penché sur le mobile de Calculair (que je ne connaissais pas (le mobile, pas Calculair que je salue)) et je n'ai pas la démonstration, mais mon "pif" me suggère que tout se passe pendant le retournement. Et non dans la seule position extrême, mais pendant tout le basculement des cylindres.
Au revoir.
La compensation n'est obligatoirement au retournement, si la hauteur est assez grande la compensation se fait sur le bras montant uniquement.
Un petit calcul pour ceux qui aiment les équations :
Le mouvement du piston peut se faire en sortie de la roue basse ou en cours de remontée si la hauteur est assez grande. Le bras de montée aura un poids supplémentaire mg sur une hauteur égale à la course du cylindre.
Il est possible de faire un calcul plus simple si l'on suppose un ressort faible ou encore le vide derrière le piston. Le travail du piston contre la pression de l'eau dans un cylindre de surface s et de course d est simplement
L a hauteur efficace sur laquelle s'applique la poussée est dans un liquide de densitévaut
La poussée d'Archimède sur un cylindre vide estet le travail de la poussée d'Archimède sur cette hauteur h est
Je remplacepar sa valeur
et j'obtiens
Donc exactement le travail qu'il a fallu fournir pour vider le cylindre.
Le système de roue est donc en équilibre. La masse supplémentaire sur le bras montant équilibre la poussée d'Archimède.
Comprendre c'est être capable de faire.

B'jour,
J'ai fabriqué la machine à pistons dans mon jardin et je peux affirmer qu'elle ne fonctionne pas.
Naaan, ch'plaisante.
En fait je l'ai fabriquée sur papier et utilisé un tableur parce que les équations ne sont pas parlantes.
J'ai considéré le cylindre comme une cloche sans piston, le piston ajoutant une différence de pression par le biais du gaz. Il faut donc trouver la différence entre la face supérieure et la face inférieure de la tête du cylindre, la hauteur h du gaz dans le cylindre dépendant de la pression sur le piston.
Pression dessus cylindre montant : Roger Zed.
Pression dessous cylindre descendant : le même.
Pression dessous cyl mont
Pression dessus cyl desc
Vous comprenez pourquoi j'ai utilisé un tableur.
pa : p atm ; q/s : pression due au poids ; ho : volume gaz à pa ; z : profondeur de la face du cylindre.
Il apparaît selon ce calcul qu'il y a un point d'équilibre, une fois atteint ça ne bouge plus.
En prenant un système à 2 cylindres la différence de hauteur pour l'équilibre diminue avec la profondeur.
Voilà. Sous réserve d'erreur parce qu'il était tard. J'y réfléchis encore.
Mais si t'as l'gosier, Qu'une armure d'acier, Matelasse. Brassens, Le bistrot.

Bonjour.
Avez vous remarqué que le piston du cylindre montant se trouve en dessous (normal d'ailleurs, et même inévitable), donc la poussée utile (celle qui est orientée vers le haut) d'archimède agit sur le piston uniquement, et l'effort est ensuite transmis au reste en comprimant l'air contenu dans le cylindre.
Alors soit le piston est si lourd que la poussée d'archimède ne peut le soulever, et il n'y a pas de poussée sur le système, soit la poussée d'archimède est suffisante pour soulever le piston et le volume diminue....................... .....
Amicalement, Alain


Bonjour.
Merci à Obi76 d'avoir séparé cet aspect de la discussion.
Je me suis lancé aussi dans le calcul.
Je suppose que le processus est isotherme:
Le piston est à la profondeur 'h' et le piston de masse 'm' et section 'S' est incliné d'un angle thêta:
Si la longueur de la zone avec de l'air est 'l', la force totale dans la direction de l'axe du cylindre est:
on remplace S.l dans cette équation:
.
Pour la montée thêta est zéro et pi pour la descente.
Comme la force calculée est en direction du cylindre, le couple par rapport aux axes des poulies et toujours 'F.r' aussi bien dans la partie droite qu'en faisant le tour des poulies. Donc, tout baigne... sauf que:
Et c'est ici où je me suis aperçu d'un petit problème et faisant la liaison avec le tour de la poulie.
La valeur de 'h' au passage droit-tour, n'est pas égale à la profondeur de l'axe de la poulie et la dépendance de 'h' avec l'angle n'est pas évidente. On peut évidemment l'écrire, mais ça devient une usine à gaz.
C'est cette même difficulté que Arrol à relevée vue d'un autre angle.
Peut-être qu'il faut choisir une autre référence que le piston. Mais je ne vois pas laquelle donne une dépendance simple entre l'angle et la profondeur du piston.
Le petit problème de Calculair est fort intéressant.
Au revoir.


Excusez moi je n'ai pas lu tous les développements mais la réponse n'est elle pas : les frottements dans les liaisons et avec le milieu, ainsi que les dissipations énergétiques dues aux déformations? Si on introduit aucune perte d'énergie je vois pas comment le système pourrait s’arrêter...

On peut même dire que si le piston est d'une densité inférieure ou égale à celle de l'eau, il ne descendra pas dans le cylindre remontant, et il n'y aura donc pas d'augmentation du volume dans le cylindre, donc pas de supplément de poussée d'Archimède, donc ça ne marche pas.Bonjour.
Avez vous remarqué que le piston du cylindre montant se trouve en dessous (normal d'ailleurs, et même inévitable), donc la poussée utile (celle qui est orientée vers le haut) d'archimède agit sur le piston uniquement, et l'effort est ensuite transmis au reste en comprimant l'air contenu dans le cylindre.
Alors soit le piston est si lourd que la poussée d'archimède ne peut le soulever, et il n'y a pas de poussée sur le système, soit la poussée d'archimède est suffisante pour soulever le piston et le volume diminue....................... .....
Amicalement, Alain
Et si le piston est d'une densité supérieure à celle de l'eau, il descendra, il y aura augmentation du volume, mais la poussée utile (celle qui est verticale de bas en haut) n'agira que sur le piston (qui représente la face du dessous). Or ce piston coulisse librement dans le cylindre et donc ne peut transmettre l'effort au système que s'il remonte en comprimant l'air dans le cylindre.
Mais puisque le piston est d'une densité > à celle de l'eau, il a plutôt tendance à couler, donc à s'opposer à la transmission de l'effort, par contre la pression s'exerçant de haut en bas sur le dessus du cylindre (toujours le cylindre montant) reste et est même dopée par la baisse de pression interne due à la descente du piston.
Amicalement, Alain

Comme je crains d'avoir été assez brouillon, je résume ainsi: Concernant le cylindre montant: soit le piston est assez lourd pour descendre et cela signifie qu'il s'oppose seul efficacement à la poussée d'Archimède et n'a donc aucune raison de transmettre le moindre effort au système, soit il n'est pas assez lourd pour descendre, et il n'y a pas d'augmentation de volume, donc pas non plus de supplément de poussée.
Amicalement, Alain


Re.Excusez moi je n'ai pas lu tous les développements mais la réponse n'est elle pas : les frottements dans les liaisons et avec le milieu, ainsi que les dissipations énergétiques dues aux déformations? Si on introduit aucune perte d'énergie je vois pas comment le système pourrait s’arrêter...
Les frottements ce n'est pas une réponse. On sait qu'en pratique ils seront toujours là. Mais s'il y a dissipation d'énergie dans les frottements, cela voudrait dire qu'il y a production d'énergie.
C'est pour cela qu'il faut (et que l'on peu) démontrer que, même en absence de frottements, le dispositif est en équilibre.
A+


Vous voulez dire que vous faites un calcul en statique ? Si le système peut être à l'équilibre alors ce n'est pas un mouvement perpétuel.
Si c'est le cas, je ne comprends pas, car si je donne une pichenette à votre système dans sa position d'équilibre il se mettra à tourner indéfiniment vu la modélisation que vous en avez faites (sans frottements).


Bonjour,
il me semble évident que n'importe quel mecanisme parfait est à mouvement perpetuel et que ce qu'il faut demontrer c'est que le systeme ne peut accelerer durablement seul , autrement dit (mais ce n'est pas la seule solution) que le travail fourni sur un cycle complet est <= 0 avec egal 0 dans le cas sans frottement.Vous voulez dire que vous faites un calcul en statique ? Si le système peut être à l'équilibre alors ce n'est pas un mouvement perpétuel.
Si c'est le cas, je ne comprends pas, car si je donne une pichenette à votre système dans sa position d'équilibre il se mettra à tourner indéfiniment vu la modélisation que vous en avez faites (sans frottements).
j'ai l'intuition que dans ce cas précis, pour faire un vilan juste du travail il faut considerer un echange de travail avec le milieu aquatique, quand un des pistons augmente de volume, on fait monter le niveau de l'eau. je pense que le bilan à un moment doit prendre en compte cela
fred

bonjour,
je profite de la mise à disposition d'in ordinateur pour suivre la discussion... Je serais chez moi fin du mois pour repondre plus finement.
Je vous remercie pour avoir eu l'idée de mettre mon super dispositif dans une discussion specifique.
Je pense qu'il faut faire un bilan rigoureux du travail des forces sur un tour complet. Les raisonnements intuitifs sont a priori favorables à la production d'energie. en effet, le système presente une symetrie par rapport à la droite passant par les axes des poulies. Le cote ou les cylindres descendent ils ont un volume plus grand, que du cote ou les cylindres remontent. Le differentiel des poussées d'archimède augmente avec le nombre de cylindre installé, et doit être suffisant pour vaincre toutes les forces de frottements, et si ve nombre de cylindre est assez grand, il semble possible d'extraire de l'energie de ce système.
Je n'ai malheureusement pas la reponse rigoureuse pour ce système pour satisfaire a la logique accademique des physiciens.
Merci à tous et à bientot
Merci pour toutes vos reflexions, je lirai toutes vos reflexions d'ici fin de mois, ou avant si je dispose d'un ordinateur.
Dernière modification par calculair ; 20/10/2011 à 08h07.
En science " Toute proposition est approximativement vraie " ( Pascal Engel)


Bonjour,
intuitivement le "loup" se situe dans les phases de retournement. Je pense que pour faire l'etude de ce systeme on peut etudier un systeme equivalent qui serait composé d'une roue et non plus d'une chaine. Autrement dit, si cela marche pour une chaine, cela doit marcher pour une roue et inversement
sur la partie montante, les masses sont en retard avec la chaine et il faudra bien rattraper ce retard a un moment donné et sur la parte descendante c'est l'inverse.
et comme archimede nous donne une relation entre la masse mobile et la poussée, j'irai chercher de ce doté la
fred


Bonjour.Vous voulez dire que vous faites un calcul en statique ? Si le système peut être à l'équilibre alors ce n'est pas un mouvement perpétuel.
Si c'est le cas, je ne comprends pas, car si je donne une pichenette à votre système dans sa position d'équilibre il se mettra à tourner indéfiniment vu la modélisation que vous en avez faites (sans frottements).
Le nom de "perpetuum mobile" fut donné à une époque ou probablement on ne savait pas ce qu'était le frottement. À l'époque tout s'arrêtait à cause des frottements et le "perpetuum mobile" était une chimère inaccessible.
Actuellement, on peut avoir un objet qui tourne éternellement. Pas sur terre, mais dans l'espace. N'importe quel corps (de préférence isolant pour éviter les courants de Foucault) mis en rotation dans l'espace interstellaire continuera à tourner indéfiniment.
On continue à donner ce nom à ce qui est, en fait, des dispositifs sur-unitaires. Des dispositifs qui fabriquent de l'énergie à partir de rien.
Donc, pour démontrer qu'un dispositif n'est pas un "perpetuum mobile", on peut ignorer les frottements et regarder si en un cycle il a gagné en énergie cinétique ou potentielle. Pour cela on peut calculer le travail fait, ou l'équilibre des forces. Le tout, sans se servir de la conservation de l'énergie.
Au revoir.


Re.
J'ai écrit des nouvelles formules, en faisant le calcul par rapport au haut du cylindre et non au piston. Et en tenant compte de l'inclinaison de cylindre (pour quand il tourne autour de la poulie). Je suis arrivé à une expression plus simple que celle trouvée par Sitalgo (post #11).
Cette fois 'z' est la profondeur du haut du cylindre. C, comme avant, est nRT.
Pour C = 0 la longueur de l'air doit être égale à zéro et le signe de la racine doit être +.
La force (vers le haut) parallèle au cylindre est:
Pour la montée et la descente le cos(theta) est nul.
Pour la rotation autour des poulies il faut remplacer 'z'
Avec z_p la hauteur de l'axe de la poulie.
Il reste à faire les 4 intégrales du travail.
Mais il me plairait que quelqu'un ait le courage de regarder si je ne me suis pas trompé.
A+

Juste une question : l'aspect thermodynamique (gaz) est-il important ? Ne peut-on faire la même chose avec le vide dans les cylindres et un ressort ? Ou encore, l'air a-t-il un autre rôle que son élasticité ?


Bonjour Amanuensis.
Je pense qu'on devrait pourvoir faire la même chose avec du vide et un ressort.
"En pratique" le changement de volume sera plus faible. Mais on s'en fout, dans la mesure où ça n'a pas de sens de faire la manip.
Mais avec le vide et un ressort, on n'aura pas à se poser la question "Et si on considère que le processus est adiabatique?" Ce qui est un sacré avantage.
Et je ne souhaite pas faire le calcul en trimbalant des gammas en exposant.
Cordialement,




Re.
J'ai trouvé une erreur dans la force.
Voici les formules corrigées:
Pour C = 0 la longueur de l'air doit être égale à zéro et le signe de la racine doit être +.
La force (vers le haut) parallèle au cylindre est:
En attendant la suivante.
A+

Salut !
Ce problème est effectivement très intéressant, d'habitude l'entourloupe est démasquée rapidement mais là ...
LPFR, il y a un élément que je ne comprend pas dans ton développement. Quand tu écris PV = C, P et V sont la pression et le volume dans le/du cylindre non ? Parce qu'ensuite, si je comprend bien, tu calcules la pression extérieure pour la substituer à P n'est ce pas ? Y a t-il une méprise de ma part ?
@+


Re.
Pour une quantité de gaz donnée à température constante PV = nRT = Cte. Quand les cylindres montent et descendent, leur piston bouge en changeant le volume pour s'adapter à la pression hydrostatique qui change avec la profondeur.
A+

Re
Oui, mais dans PV = C tu remplace P par rho g h qui est la pression extérieure au cylindre alors qu'initialement dans PV = C, P est la pression à l'intérieur du cylindre. Les deux pressions ne sont pas égales. Si ?
@+

