La gravité est nulle à l'intérieur d'une coquille sphérique homogène

[triall]

L' attraction gravitationnelle que l' atmosphère exerce sur nous est nulle , mais ça ne nous enlève pas la pression atmosphérique due au poids de tout l' air qui se trouve au dessus de nous .
C' est deux choses différentes .
Le magma ne subit pas l' attraction des roches au dessus de lui mais il subit les effets de leur poids .

Oui, je pense que c'est ça .C'est ce que j'essayais d'expliquer avec mes gaillards qui me pressent de part et d'autres de l'épaule . Une gravitation nulle ne veut pas dire pas de gravitation , comme au final, 2 forces qui s'annulent ne veut pas dire qu'il n'y a pas de force .
Pour ce qui est de la démonstration de LPFR, je regrette qu'il aille si vite en "besogne" son équation, même si elle est alléchante, ne me parait pas bonne .Je me demande si beaucoup de personne comprend cette expression de la masse ? le cos théta me pose problème, ainsi que la multiplication par L₁²
Pour me permettre de prendre un peu de temps , voilà ce que j'ai, au départ noté pour la gravitation :

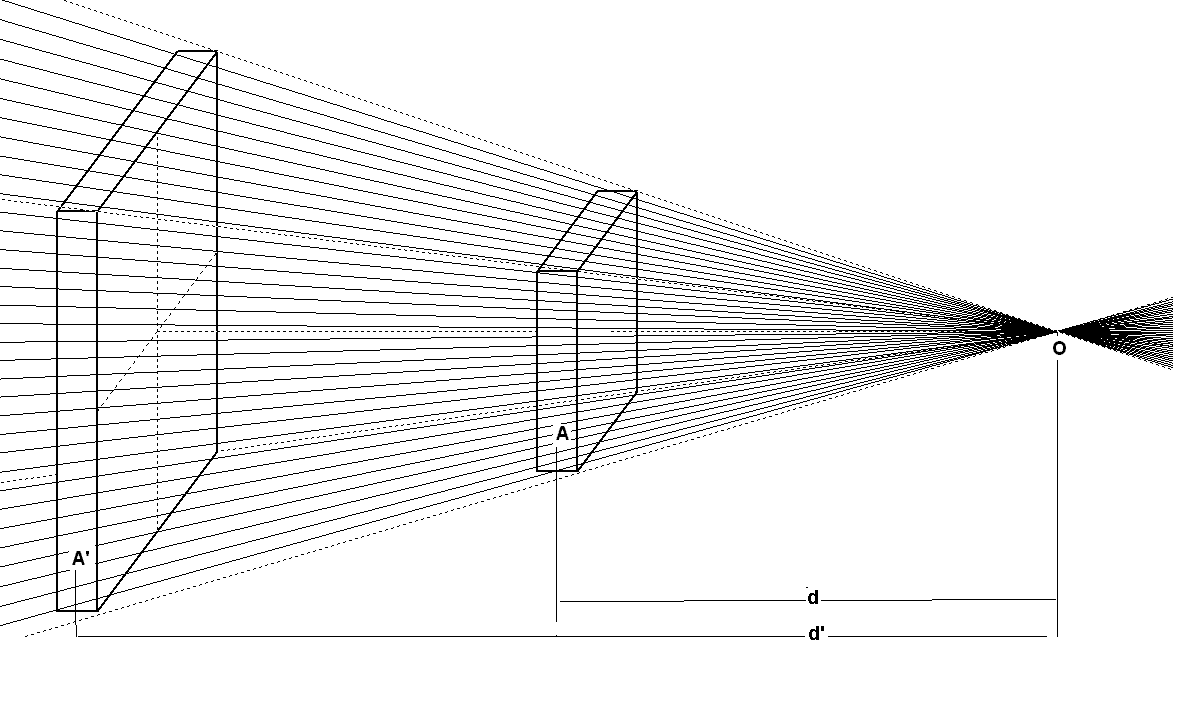
On démontre facilement dans ce cas simple que la masse test placée en O subit la même force d'attraction de la part des 2 cubes A' et A à sa gauche, à cause de la loi en 1/d² et de l'égalité d'épaisseur des cubes . Le rapport m'/d'²=m/d² .m masse de A et m' masse de A' .Vous suivez ?
Ainsi , bien entendu tout cube présent dans ce cône , et d 'épaisseur identique provoque la même attraction sur O , même placé à droite .
Je ne sais pas tracer de cône circulaire avec mon logiciel de dessin , mais je vous invite à penser que pour la sphère, et le point M on est à peu près dans le même cas de figure , l'épaisseur étant identique ..Je développerai plus ...
-----

[triall]

Bonjour ,@lpfr .
J'ai un grand respect pour votre science et votre culture , très sincèrement , voire une certaine "admiration" .Vous répondez rapidement à pratiquement toutes les interrogations que se posent les forumeurs .
Pour ce qui est du théorème de Gauss , votre démonstration est trop courte, elle est peut -être valable, mais ,il me semble , qu'elle mérite plus d'explications .Je crois que l'on a là une manifestation de la force de gravitation qui nous "montre" quelque chose avec cette propriété théorique trouvée par Gauss .
Je n'arrive pas bien à comprendre vos équations, surtout lorsqu'elles entrent dans la "limite" avec la division par cos (théta) ; mais elles semblent "vraies" pour des valeurs "normales" aux alentours du passage par le diamètre (théta=0°) et le cos(théta)=1...
A suivre, s'il vous plait .

[coussin]

https://en.wikipedia.org/wiki/Shell_theorem
La démonstration de LPFR.

[LPFR]

Bonjour ,@lpfr .
J'ai un grand respect pour votre science et votre culture , très sincèrement , voire une certaine "admiration" .Vous répondez rapidement à pratiquement toutes les interrogations que se posent les forumeurs .
Pour ce qui est du théorème de Gauss , votre démonstration est trop courte, elle est peut -être valable, mais ,il me semble , qu'elle mérite plus d'explications .Je crois que l'on a là une manifestation de la force de gravitation qui nous "montre" quelque chose avec cette propriété théorique trouvée par Gauss .
Je n'arrive pas bien à comprendre vos équations, surtout lorsqu'elles entrent dans la "limite" avec la division par cos (théta) ; mais elles semblent "vraies" pour des valeurs "normales" aux alentours du passage par le diamètre (théta=0°) et le cos(théta)=1...
A suivre, s'il vous plait .

Bonjour.
L’angle solide dΩ sous lequel on voit une surface dS de petites dimensions situé à une distance R est



Où thêta est l’angle formé par la perpendiculaire à la surface et le segment ‘R’ (0° quand la surface est vue perpendiculairement).

Donc, dans notre cas



La masse dm d’une telle surface est égale à où rhô est la densité (absolue !) et ‘e’ l’épaisseur.
Et dans mon post j’ai appelé σ = ρ.e, la masse par unité de surface.

Donc, pour le problème que vous avez posé, l’attraction de gravité ne dépend pas de la distance, pour un même angle solide. Et comme les deux thêtas sont égaux, les forces se compensent.
Au revoir.

[triall]

Bonjour, oui ,j'avais compris mais comment justifiez -vous que votre masse vue ..tende vers l'infini quand théta tend vers 90° !

[LPFR]

Bonjour, oui ,j'avais compris mais comment justifiez -vous que votre masse vue ..tende vers l'infini quand théta tend vers 90° !

Re.
Quand est ce que thêta tend vers zéro ?
Quand le point tend vers la surface (plutôt le milieu de l’épaisseur) de la coquille.
Donc, la masse ne tend vers l’infini, car la distance à la coquille tend aussi vers zéro.
A+

[triall]

@LPFR , oui, j'avais compris que théta tend vers 90 et non zéro lorsque le point est sur le cercle intérieur de la coquille ;cercle passant par BB' ; donc d'accord ; la distance à la coquille tend aussi vers 0 , mais je ne vois pas dans votre expression cette distance, vous parlez de e l'épaisseur ...Quelle est l'expression de la distance du point M au cercle intérieur (c'est bien de cette distance dont on parle qui tend vers 0 lorsque le point est sur ce cercle intérieur) .Vous parliez, il me semble de la distance au cercle extérieur ....
Je vous invite, s'il vous plait , pour la suite à m'aider à trouver une expression du volume , puis de la masse d'une portion de coquille , d'un angle solide oméga , et d'un angle thétha comme vous l'avez indiqué, angle que fait la droite avec un des 2 cercles ,sans la notation infinitésimale qui est superfétatoire (20 points pour ce mot )
Pour coussin, dans le lien que vous indiquez, je ne vois pas de ..coquille sphérique sur les dessins !

[LPFR]

@LPFR , oui, j'avais compris que théta tend vers 90 et non zéro lorsque le point est sur le cercle intérieur de la coquille ;cercle passant par BB' ; donc d'accord ; la distance à la coquille tend aussi vers 0 , mais je ne vois pas dans votre expression cette distance, vous parlez de e l'épaisseur ...Quelle est l'expression de la distance du point M au cercle intérieur (c'est bien de cette distance dont on parle qui tend vers 0 lorsque le point est sur ce cercle intérieur) .Vous parliez, il me semble de la distance au cercle extérieur ....
Je vous invite, s'il vous plait , pour la suite à m'aider à trouver une expression du volume , puis de la masse d'une portion de coquille , d'un angle solide oméga , et d'un angle thétha comme vous l'avez indiqué, angle que fait la droite avec un des 2 cercles ,sans la notation infinitésimale qui est superfétatoire (20 points pour ce mot )
Pour coussin, dans le lien que vous indiquez, je ne vois pas de ..coquille sphérique sur les dessins !

Re.
La notation infinitésimale est nécessaire. À la rigueur vous pouvez remplacer els différentiels par des Δ. Car si la petite surface ne peut pas être considéré comme plane, on peut difficilement de parler d’angle entre la droite BB’ ou AA’ et la surface.
Le volume d’une couche mince d’épaisseur uniforme, qu’elle soit sphérique ou tarabiscotée est égal à la surface par l’épaisseur (comme le volume du mouchoir que vous avez dans votre poche).
Et la masse est égale à la masse volumique (que j’appelle toujours densité) multipliée par le volume.

Prenons pour simplifier (les angles) le point M au milieu segment AA’.
L’angle que AA’ fait avec le rayon OA est précisément thêta (le même qu’avant).
Et R cos (thêta) = MA (avec R = rayon du cercle)
Si je reprends la formule du post #34 en remplaçant R par MA



Donc, quand cos(thêta) tend vers zéro, l’ensemble tend vers zéro et non vers infini.

Dans le lien de Wikipedia, la démonstration est la même que celle que j’ai mise dans mon fascicule de mécanique et que j’avais pompée du Resnick. Rien à voir avec celle que j’ai donnée ici (et que j’ai probablement lu quelque part il y a bien longtemps),
A+

[triall]

Bonsoir, à tous, désolé lpfr, mais je ne vois pas immédiatement ce dont vous voulez parler .
Reprenez le terme de la masse en dm si vous voulez , on a un diviseur en cos(tétha) qui évidemment tend vers 0 .... lorsque le point M s'approche du cercle intérieur et que son angle tend vers 90°,mais, je ne vois pas en haut de terme qui tende vers 0 .Quand bien même , personne ne dit que 0/0 en math donne 1 , cela dépend.
Je ne lâche rien, même si je suis d'accord , évidemment sur la conclusion ; la gravité s’annule à l'intérieur d'une coquille sphérique ; votre démonstration me laisse perplexe !Vous savez, mieux que moi , qu'une proposition peut être vraie (p implique q est vraie sans que q implique p soit vraie )
S'il vous plait (re) donnez l'expression de la masse d'un angle solide oméga vue d'un point M . Très franchement, je n'ai pas compris, je repose ma question "Qui a compris ?" et essayez d'expliquer , on parle de force ressentie de part et d'autre d'un point M , sur une sphère , et on est d'accord , cette force est forcément égale à droite et gauche, on a ainsi une force de gravitation nulle comme je le montre sur le dessin plus haut message 16 dont la cause est l'égalité des distances AB et A'B ' .
Je vous ai fourni un dessin sur le message 31qui montre aussi en première approximation que sur une sphère les forces s'annulent à droite et gauche .

[Dynamix]

L' élément de surface étant très petit , il est équivalent à un plan .
On prend un cône d' angle solide dΩ et on le coupe par un plan normal à l' axe , l' intersection , c' est dS , avec θ = 0
On incline le plan . dS s' agrandit (ou si dS est constant , c' est dΩ qui rapetisse)
Quand θ tend vers 90° dS tend bien vers l' infini .
Mais après tu le fait tendre vers zéro , donc c' est juste ponctuel .

[triall]

Bonsoir, "ne noyez pas le poisson" dynamix, et indiquez moi , s'il vous plait , quel est le terme, au numérateur :la partie haute de la division pour l'expression de la masse vue de M avec l'angle oméga qui tend vers 0.(terme qui tendrait vers 0 et qui annulerait donc le terme au dénominateur(en bas) qui tend vers 0 aussi avec cos(tétha) tétha qui tend vers 90 , lui quand M se rapproche du cercle intérieur ?Le seul terme en distance que je vois au numérateur est l'épaisseur de la coquille, qui ne tend pas vers 0 et qui est constante évidement . Avec donc , en prime le théorème très connu 0/0 =1
Quel est donc ce terme au numérateur dans l'expression de la masse qui tend vers 0 lorsque théta tend vers 90° et non vers 0 ;attention c'est cos 90° qui tend vers 0 , et donc lorsque tétha tend vers 90°!!!!

Pour le lien de coussin, en anglais , je le répète , je ne vois pas de coquille(au sens géométrique) dans les dessins , ce n'est pas le théorème de Gauss dont il s'agit; théorème qui parle de coquille sphérique !!!!!
Bonne journée .

[pointcare2]

on peut raisonné par les symetries spherique : le centre de la terre est l'intersection de trois plans de symetrie indepandants

[pointcare2]

[LPFR]

Bonsoir, à tous, désolé lpfr, mais je ne vois pas immédiatement ce dont vous voulez parler .
Reprenez le terme de la masse en dm si vous voulez , on a un diviseur en cos(tétha) qui évidemment tend vers 0 .... lorsque le point M s'approche du cercle intérieur et que son angle tend vers 90°,mais, je ne vois pas en haut de terme qui tende vers 0 .Quand bien même , personne ne dit que 0/0 en math donne 1 , cela dépend.
Je ne lâche rien, même si je suis d'accord , évidemment sur la conclusion ; la gravité s’annule à l'intérieur d'une coquille sphérique ; votre démonstration me laisse perplexe !Vous savez, mieux que moi , qu'une proposition peut être vraie (p implique q est vraie sans que q implique p soit vraie )
S'il vous plait (re) donnez l'expression de la masse d'un angle solide oméga vue d'un point M . Très franchement, je n'ai pas compris, je repose ma question "Qui a compris ?" et essayez d'expliquer , on parle de force ressentie de part et d'autre d'un point M , sur une sphère , et on est d'accord , cette force est forcément égale à droite et gauche, on a ainsi une force de gravitation nulle comme je le montre sur le dessin plus haut message 16 dont la cause est l'égalité des distances AB et A'B ' .
Je vous ai fourni un dessin sur le message 31qui montre aussi en première approximation que sur une sphère les forces s'annulent à droite et gauche .

Bonjour.
Revoyez la démonstration du post#38. J’arrive bien à 0/0 mais c’est parce que je vous ai laissé simplifier cos²/cos, ce que vous n’avez pas fait. Mais, si vous le faites, vous ne trouverez qu'un simple cos au numérateur et qui tend vers zéro quand le point M tend vers la coquille.
Au revoir.

[triall]

Bonjour à tous.

On s'embrouille LPFR; au cas où M est au milieu de AA'comme sur le dessin, il n'y a plus de problème, il est évident que les 2 masses contenues d'une part dans ABCD et d'autre part dans A'B'C'D' de l'autre côté sont égales !!!A cause aussi, évidement des égalités triviales AB=A'B' et CD=C'D'
Mais je ne vois pas la surface ABCD=R²cos(thêta) , de quel rayon R s'agit-il du petit ou du grand ?
Sur mon dessin en haut j'ai mis thêta =90 , mais la surface dS serait plutôt AB² à mon avis! .Il existe aussi une "embrouille" pour thêta , il est possible que ce soit le complémentaire , mais cela ne change rien , il y a un problème avec la surface ...
Pour le volume je pense alors qu'il faut multiplier la surface par AB et pour la masse par rhô .(rhô densité de la coquille)
La masse est donc ds.AB rhô , mais je ne suis pas d'accord avec votre expression de dS .
Sinon , prendre M au milieu de AA' c'est évidement se faciliter la tâche , les 2 masses à droite et gauche sont évidement égales .
Pourquoi ne pas se cantonner aussi à M sur le centre de la coquille ?
Je suis très intéressé par une expression de la masse vue de M quelconque dans le petit angle solide, mais il "'suffit" de démontrer pour un point M quelconque que le rapport masse/d² est identique de part et d'autre d'un angle solide quelconque, comme montré sur mon message 31.
Il faut se "persuader" que l'on a le même cas de figure sur une coquille sphérique .
Bonne journée

[sitalgo]

B'jour,

on parle de force ressentie de part et d'autre d'un point M , sur une sphère , et on est d'accord , cette force est forcément égale à droite et gauche, on a ainsi une force de gravitation nulle comme je le montre sur le dessin plus haut message 16 dont la cause est l'égalité des distances AB et A'B ' .

Certainement pas. Les champs gravitationnels sont identiques mais à des origines différentes. Le seul endroit où les champs s'annulent est le point de Lagrange. Le point M n'est donc pas en équilibre.
L'explication est bien insuffisante. Considérer un angle solide comme le dit LPFR est suffisant.

Je vous ai fourni un dessin sur le message 31qui montre aussi en première approximation que sur une sphère les forces s'annulent à droite et gauche .

Dessin qui montre que tu as compris le principe or dans le message 16 cela impliquerait que 2 carrés de mêmes dimensions mais à distance différente de M créeraient la même force. C'est contradictoire.

Inutile de compliquer en donnant une épaisseur à la sphère, ça ne change rien.

[triall]

@sitalgo Dessin qui montre que tu as compris le principe or dans le message 16 cela impliquerait que 2 carrés de mêmes dimensions mais à distance différente de M créeraient la même force. C'est contradictoire.
Pour le dessin message 36 , 2 carrés ne peuvent être de même dimension , s'ils ont des distances différentes ;
Il est évident, dans ce dessin(j'ai la démonstration) que le rapport m/d² est constant le long du cône, quand les carrés-parallélépipèdes ont une même épaisseur .
Je me rends compte que j'écris aussi des coquilles, dans le dessin précédent M est milieu de AB' et non de AA'
Sinon, pour repartir sur de "bonnes bases" voici un dessin avec oméga, thêta......Si la coquille n'a pas d'épaisseur , je me demande à quoi ça sert d'énoncer le théorème de Gauss !
Ca me semble compliqué de donner une expression de la surface, puis volume en fonction de thêta de la portion de cône ABCD d'angle solide oméga ,

[Dynamix]

indiquez moi , s'il vous plait , quel est le terme, au numérateur :la partie haute de la division pour l'expression de la masse vue de M avec l'angle oméga qui tend vers 0

NIET !
Je préfère faire tendre dS vers zéro .
A ldSl constant , quand j' incline dS , dΩ tend vers zéro .
Autrement dit , l' angle solide devient ponctuel .
Normal vu qu' il s' agit d' une tangence .

[triall]

Bonjour à tous, c'est ce que j'appelle "se faire pourrir" , je me le fais copieusement(pourrir) car; je ne peux répondre à tous , je vous invite alors (puisque c'est "mon" post ) à dorénavant commenter le dessin fourni juste précédemment ;avec les notations; et à être le plus précis possible dans vos formulations .
Par exemple , Sitalgo me dit que l'épaisseur n'intervient pas , qu'il me dise plutôt que l'épaisseur de la coquille peut ne pas entrer en jeu dans la démonstration là je comprendrais mieux;mais qu'il le démontre; et le poste précédent de dynamix est incompréhensible pour moi !
Cette expression, par exemple :

A ldSl constant

??

[sitalgo]

Dans l'attente de validation du dessin,

Pour le dessin message 36 , 2 carrés ne peuvent être de même dimension , s'ils ont des distances différentes ;

Il est évident, dans ce dessin(j'ai la démonstration) que le rapport m/d² est constant le long du cône, quand les carrés-parallélépipèdes ont une même épaisseur .

Inutile d'expliquer cela, j'ai dit que le message 36 était bon mais le dessin du message 16 associé au message 39 "on parle de force ressentie de part et d'autre d'un point M , sur une sphère , et on est d'accord , cette force est forcément égale à droite et gauche, on a ainsi une force de gravitation nulle comme je le montre sur le dessin plus haut message 16 dont la cause est l'égalité des distances AB et A'B ' ", ça ne colle pas.

Par exemple , Sitalgo me dit que l'épaisseur n'intervient pas , qu'il me dise plutôt que l'épaisseur de la coquille peut ne pas entrer en jeu dans la démonstration là je comprendrais mieux;mais qu'il le démontre

Une coquille ayant une épaisseur, c'est la somme des coquilles d'épaisseur élémentaire, pour le cas présent les conséquence d'une s'applique à l'autre. Mais bon, c'est peut-être important pour le suite de ta démonstration.

[Dynamix]

le poste précédent de dynamix est incompréhensible pour moi !
Cette expression, par exemple :A ldSl constant

J' en suis désolé .
ldSl (scalaire) c' est l' aire de la surface orientée dS (vecteur)
Si on découpe S en n petits carrés d' aire ldSl , suivant le point ou on se place on aura toujours les même ldSl , mais pas les même dS , donc pas les même angles solides .

Pour l' épaisseur , il suffit de prendre une épaisseur dr et d' integrer de r1 à r2
Une intégrale de volume , c' est plus logique pour calculer une force gravitationnelle .

[sitalgo]

À première vue la remarque de LPFR m'a parue suffisante, cependant il ne me paraît pas évident que lorsque M se déplace sur la ligne, les surfaces et a fortiori les volumes restent (pile-poil mathématiquement) en accord avec le rapport en 1/d² vu que ce ne sont pas des surfaces planes. Je suis incapable de le dire.

[LPFR]

Re.
Je n’ai pas le temps de répondre maintenant. Je le ferai en fin d’après-midi.
A+

[triall]

@lpfr ; j'aimerais que vous répondiez précisément à mes questions ; non pour vous "harceler" , car c'est moi qui suis dans cette position actuellement , mais pour essayer de progresser .
Le fait d'avoir parlé de surface massique m'a fait beaucoup progressé , car je ne connaissais pas cette notion .
Maintenant quand vous mettez le point M au milieu de AA' , je vous cite, sur le dessin message 16 ; évidemment la masse est égale de part et d 'autre de M . Indiquez clairement que vous vous êtes trompé , cela vous arrive aussi, moins souvent que la moyenne ; bien moins souvent que moi , mais il faut savoir reconnaître votre erreur , ou connerie, vous l'avez fait plusieurs fois et bravo , c'est normal , si vous répondez à 10 questions /jours vous avez plus de chance de vous tromper que ceux qui ne répondent qu'à une question/jour ou 0 question/jour !!
Le problème, et je reconnais cette erreur c'est que dans le dessin plus loin, j'ai interverti A , A' , alors que A' devrait rester sur le cercle extérieur , il est passé sur le cercle intérieur !
Je vous invite donc, à partir de maintenant de noter les points comme indiqué dans le dernier dessin message 47 ; et reconnaître que mettre le point M au milieu est une ...connerie .
Bonne journée .

[coussin]

Dans ce pdf, il me semble qu'il y a la démonstration avec les angles solides. Ça semble d'ailleurs être la démonstration dûe à Newton.

[sitalgo]

Dans ce pdf, il me semble qu'il y a la démonstration avec les angles solides. Ça semble d'ailleurs être la démonstration dûe à Newton.

Bon, ben alors ça roule.

[triall]

Rebonjour, coussin nous sommes sur un forum et il est très intéressant de dialoguer avec des propositions(plus ou moins) personnelles ; le niveau de la discussion me satisfait de la part de coussin, LPFR, Dynamix , sitalgo ; poincarre2(je m'excuse, impossible de répondre , développez svp !) and Co dans la mesure où on se réfère à un dessin, il s'agit maintenant du dessin message 47 .
Merci de ne plus maintenant se référer à un pdf sur wikipédia ou autre source, même si je respecte profondément cette source , on en est à un point où chacun doit démontrer personnellement ce qu 'il dit, et je préfèrerais la méthode géométrique avec le dessin fourni message 47 ...
Bonne journée

[Dynamix]

il ne me paraît pas évident que lorsque M se déplace sur la ligne, les surfaces et a fortiori les volumes restent (pile-poil mathématiquement) en accord avec le rapport en 1/d² vu que ce ne sont pas des surfaces planes. Je suis incapable de le dire.

Quand tu fais tendre dS vers zéro , le défaut de planéité (du second ordre ) disparaît .

[coussin]

Rebonjour, coussin nous sommes sur un forum et il est très intéressant de dialoguer avec des propositions(plus ou moins) personnelles ; le niveau de la discussion me satisfait de la part de coussin, LPFR, Dynamix , sitalgo ; poincarre2(je m'excuse, impossible de répondre , développez svp !) and Co dans la mesure où on se réfère à un dessin, il s'agit maintenant du dessin message 47 .
Merci de ne plus maintenant se référer à un pdf sur wikipédia ou autre source, même si je respecte profondément cette source , on en est à un point où chacun doit démontrer personnellement ce qu 'il dit, et je préfèrerais la méthode géométrique avec le dessin fourni message 47 ...
Bonne journée

Votre réaction est étrange... Votre dessin du message #47 est reproduit en fig 1 du pdf de mon dernier message. Que vous faut-il de plus?
Votre entêtement devient ridicule, je dois dire...

[LPFR]

Re.
Le pdf donné par Coussin au post #55 fait la démonstration de ce que l’on est en train de discuter ici. Et il la fait de façon très très détaillée (8 pages !).
Il arrive, comme moi, à un cos(thêta) au dénominateur, ce qui ne pose pas des problèmes car le numérateur tend vers zéro encore plus vite que le dénominateur quand cos(thêta) tend vers zéro.

Je vous ai donné la démonstration en me simplifiant la vie en prenant le point de mesure (M) au milieu du segment.
Et cela ne vous a pas plu.
Essayez donc, de faire un dessin avec thêta qui tend vers 90° (cela veut dire que le segment tend à devenir tangent à la coquille). Essayez de vous demm…brouiller pour que le segment tende à être tangent à la coquille et que le point de tangence ne tende pas vers le milieu du segment. Vous aurez du mal.
A+