La gravité est nulle à l'intérieur d'une coquille sphérique homogène

[triall]

Bonjour, attention il s'agit de la gravité due aux parois de la coquille et non une gravité extérieure qui s'annulerait.La gravité n'est pas nulle dans une boule de pétanque creuse sur Terre . Je crois que c'est un théorème de Gauss .
Par exemple ,quand on s'enfonce dans la Terre , puits de pétrole, grotte, on ne compte pas la gravité de ce qui est au dessus de nous , la gravité est causée par tout ce qui est en dessous , vers le centre de la Terre .(en considérant la Terre comme une sphère homogène)

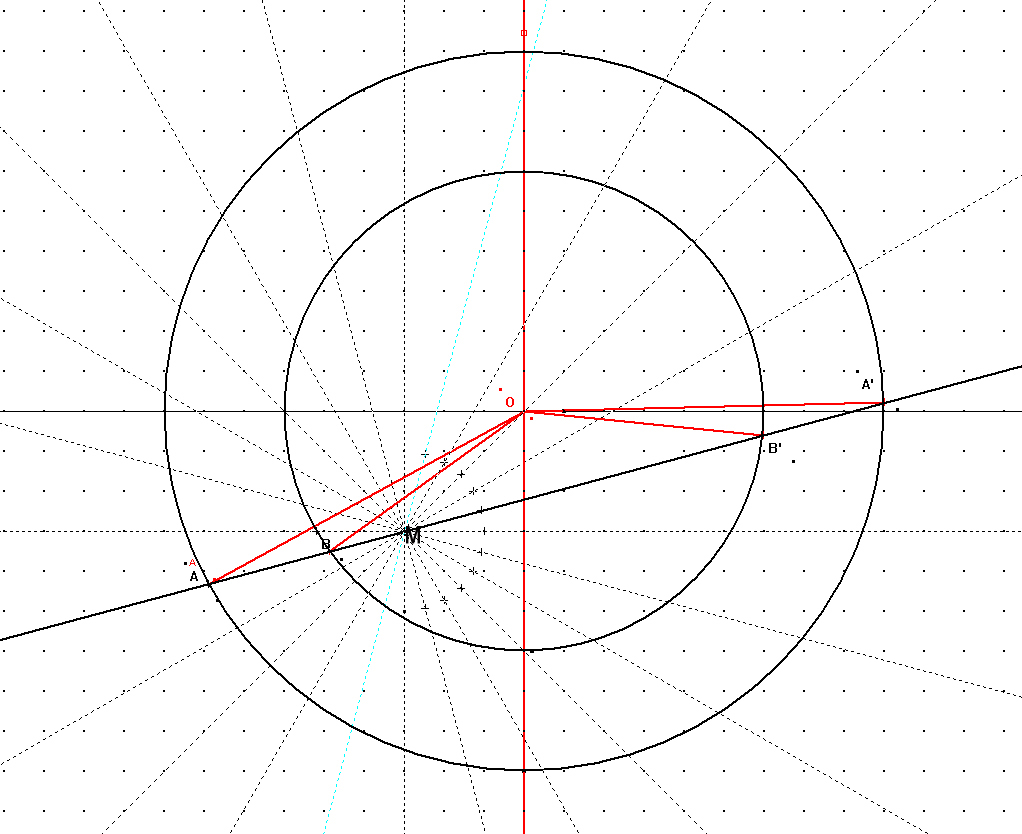
En me penchant sur ce théorème, et en essayant de le comprendre, j'ai trouvé une explication géométrique assez triviale ; je vous invite à trouver laquelle.
-----

[albanxiii]

Bonjour,

Angle solide.

@+

[triall]

J'ai l'impression qu'albanxii connait la réponse,merci de ne pas dévoiler tout de suite; je l'invite à trouver néanmoins une propriété encore plus "primaire", et laisser un peu durer le post !

[LPFR]

Bonjour.
Je pense qu’il y a deux : l’angle solide et les angles d’intersection de la surface d’une droite qui traverse la coquille.
Au revoir.

[A voir en vidéo sur Futura]

[coussin]

C'est une propriété géométrique des forces en 1/r2.

[triall]

Oui, albanxii, coussin, Lpfr c'est la voie .
Il y a une propriété essentielle et triviale d'une droite quelconque qui coupe la coquille sphérique......

[Obamot]

Arf, ça me rappelle le "calcul des moments" (en statique et résistance des matériaux): F x bras de levier, le tout ramené à une sphère ... pas évident de le calculer, dès lors que les forces se répartissent et finissent par s'annuler entre-elles... De là à dire que la gravité intrinsèque serait nulle(?) pour une coquille sphérique homogène: voilà qui est très intéressant!

[triall]

Bonsoir, oui, obamot , c'est , selon moi , très intéressant !
Pour être un peu plus clair, le théorème de Gauss parle de la force de gravitation à l'intérieur d'une coquille sphérique .Imaginons un quidam à l'intérieur de cette coquille , en dehors de toute sorte d'autre attraction.Le théorème indique que pour ce quidam, l'attraction qu'exerce les parois sur lui même s'annule , même si ces parois ont une masse importante , du moment qu'elles sont homogènes, de même densité .Le quidam , quelque soit sa position à l'intérieur de la sphère , au milieu, au bord , est "attiré" de la même façons sur les parois, de manière à ce que la somme de ces attractions soit nulle ! Il flotte donc à l'intérieur de cette coquille sphérique , sans gravité apparente !

[Dynamix]

pas évident de le calculer, dès lors que les forces se répartissent et finissent par s'annuler entre-elles...

Justement , il n' est pas nécessaire de les calculer , il faut juste montrer qu' elles s' annulent avec leur vis à vis .

[triall]

Justement , il n' est pas nécessaire de les calculer , il faut juste montrer qu' elles s' annulent avec leur vis à vis .

Bien vu Dynamix; et la démonstration est assez simple avec de la géométrie de base , et donc comme indiqué, une propriété élémentaire d'une droite coupant une coquille sphérique !

[albanxiii]

Re,

et laisser un peu durer le post !

C'est quand c'est long que c'est bon, en effet

Bien vu Dynamix; et la démonstration est assez simple avec de la géométrie de base , et donc comme indiqué, une propriété élémentaire d'une droite coupant une coquille sphérique !

C'est justement ça que je trouve plus facile à visualiser avec les angles solides.

@+

[triall]

@albanxii , oui les angles solides entrent en jeu après, mais d'abord il y a une propriété de base d'une droite quelconque coupant une coquille sphérique, sauf coquille c'est la cause élémentaire, je crois, de cet effet d'annulation du champ de gravité à l'intérieur de la coquille

[Obamot]

Difficile à expérimenter cependant... Il faudrait être loin de tout champ gravitationnel (d'attraction massique de même valeur, donc en orbite «à l'altitude qui va bien» ! Bein tu vois Dynamix, il peut être nécessaire de le calculer, hihihihi) Et si je flottais dedans avec un scaphandre*, alors je constituerais une masse plus importante que le contenant... Que se passerait-il alors? Un collapse de la coquille(?) *

C'est la première fois que je vois une représentation de la loi de masse (masse spécifique x surface: m' en kg/m2 VS 1/r2) être en mesure d'expliquer son implication avec un champ gravitationnel alors qu'il en est partie intégrante... wow!!



Encore.. Encore...


* (Sans scaphandre on peut enlever le "je")

[Obamot]

(suite) Je m'y perds un peu... Admettons que la coquille soit en calcaire (ou sulfate de calcium, donc en "plâtre") est-ce que le type de matériaux pour la coquille joue un rôle? selon le diagramme ci-dessus, on voit qu'une coquille même de ce type serait néanmoins résistante, et aurait pas loin de la masse surfacique du béton

La transmission des efforts quant à elle peut varier, le béton le supporte très bien à la compression (pas à l'étirement) alors que l'acier supporte très bien les deux (compression et étirement, il a la dureté du béton et la flexibilité idéale du métal, pour une sphère...).

De là j'en viens à ma question, est-ce qu'une sphère ajourée en charpente métallique (en épure de Cremona) annulerait aussi la gravité à l'intérieure de sa structure?

[triall]

Bonsoir, ce théorème de Gauss n'a pas beaucoup de retombées pratique, sauf de calculer le champ de gravitation à l'intérieur de la Terre .
Comme je l'indiquais, ce théorème implique que quand on descend sous Terre , les roches qui se trouvent au dessus de nous ne comptent pas , la gravité dépend uniquement de tout ce qui se trouve en dessous (en considérant a Terre comme une sphère homogène) ; ce qui s'énonce comme "Le champ de gravitation est nul (s'annule) à l'intérieur d'une coquille sphérique homogène" ; il s'agit de l'attraction des parois sur une masse m de référence à l'intérieur de la coquille !
Comme c'est parti, je vais bien me faire "pourrir" , car la solution géométrique de ce théorème de Gauss est relativement simple ; mais j'adore ça (me faire pourrir !") .
Trouvez donc , d'abord ,la propriété simple qu 'a une droite quelconque qui coupe une coquille , je vous livre ensuite mon raisonnement géométrique (avec les angles solides)qui conduit au théorème de Gauss .......

[triall]

Bonjour à tous.
Bon, alors prenons une masse test , ou un point à l'intérieur de la coquille sphérique et traçons une droite quelconque .
Cette droite coupe la coquille en 2 endroit opposés .On montre facilement que les distances traversées par la droite sont égales, pour chaque droite :
Démonstration : voici une coquille sphérique de rayon OA et OB . D'un point M quelconque, je trace une droite d qui coupe la coquille en AB et A'B' ...Je crée un plan qui passe par cette droite d et par le centre de la coquille .Voilà ce que ça donne :

Je considère les triangles OAB et OA'B' , 2 côtés égaux, déjà .le triangle OBB' est isocèle (2 rayons) , alors l'angle OBM= angle OB'M , alors angleABO= angleOB'A' .

Les triangles OAB et OA'B' ont 2 côtés égaux, et un angle égal, ils sont égaux et AB=A'B' ! .En fait , on pouvait se passer de cette démonstration en notant que chaque droite qui passe par M coupe la sphère en 2 endroit symétriques, et la distance de traversée de cette coquille à droite et gauche est forcément identique. Ainsi le passage à la démo 3 D est évident , comme toute droite qui coupe la coquille, la coupe suivant une distance égale .
C'est ça la propriété triviale d'une droite qui coupe une coquille sphérique , attention la distance de coupe varie pour chaque droite, mais ce qui est important c'est qu'elle soit égale de part et d'autre pour chaque droite .
Je prétends que c'est cette propriété qui implique que le champ de gravitation s'annule à l'intérieur d'une coquille sphérique .On peut imaginer une très grande coquille, avec une paroi conséquente , et un quidam à l'intérieur, ce quidam sera également attiré par les parois de la coquille, de sorte qu'au final la force d’attraction s'annule, notre quidam "flotte" dans sa coquille !!!!
S'il vous plait essayez d'expliquer(ou me rétorquer) pourquoi c'est cette propriété soulignée qui fait que le champ soit nul ....
Bonne journée .

[LPFR]

Bonjour.
Non. Cette propriété ne suffit pas, comme je l’ai dit au début. Il faut aussi utiliser les propriétés des angles solides.
La masse vue par un petit angle solide dOmega autour de la droite vaut :



Où thêta est l’angle entre la droite et la surface (90° pour un diamètre et 0 pour une tangente). Sigma, la densité surfacique de masse et l₁, la distance du point à la surface.
La force d’attraction est égale à ça multiplié par G et divisé par l₁²
Donc :



Donc, pour le côté opposé la force est la même et de direction opposée
Au revoir.

[coussin]

Et comme je l'ai dit il faut que la force soit en 1/r2...

[LPFR]

Et comme je l'ai dit il faut que la force soit en 1/r2...

Re.
C'est "souvent" le cas pour la gravitation.
A+

[coussin]

On se sert d'ailleurs de cet effet pour vérifier que la gravité est une force en 1/r2

[coussin]

Oops, correction : on se sert de cette propriété pour vérifier que la force de Coulomb est en 1/r2 Difficile de faire l'expérience pour la gravité

[triall]

Bonjour, @coussin, oui, j'ai omis de dire que cela dépendait aussi de Newton !
Lpfr nous sort une magnifique équation,je m'y attendais; avec la masse surfacique (je dois avouer que je n'en avais jamais entendu parler ) , c'est bien vu , et cela évite de parler de l'égalité des distances AB et A'B' .
Néanmoins, je suis un peu gêné de voir l'expression de la masse divisée directement par cos (théta) , cela voudrait dire que pour théta =90° la masse serait infinie, ce qui n'est évidement pas le cas ! Il me semble aussi que c'est plûtôt 0° pour le diamètre et 90° pour la tangente...
Qu'une force devienne théoriquement infinie à cause du terme en 1/d² cela se conçoit , 2 atomes ne peuvent se toucher et ça montre le caractère forcément discontinu de la force de gravitation ....
Je fournirai " ma" démonstration, vous vous en doutez un plus plus géométrique et" physique avec les mains" ; "ma démo" il me semble ne fait intervenir que l'égalité de distance de coupe et Newton , bien sûr .
Pour la vérification du théorème, je pense que la descente sous Terre ou sous l'eau et la mesure de g devrait donner des indications, bien que la croute terrestre ne soit pas vraiment homogène ....(eau -roche ...)

[Dynamix]

Néanmoins, je suis un peu gêné de voir l'expression de la masse divisée directement par cos (théta) , cela voudrait dire que pour théta =90° la masse serait infinie, ce qui n'est évidement pas le cas !

C' est bien le cas si la droite est tangente à la surface .
Mais "90° pour un diamètre et 0 pour une tangente" , il me semble que c' est l' inverse .

[coussin]

http://en.wikipedia.org/w/index.php?...of_Earth#Depth

[Amanuensis]

Néanmoins, je suis un peu gêné de voir l'expression de la masse divisée directement par cos (théta) , cela voudrait dire que pour théta =90°

Pas possible pour un point strictement à l'intérieur.

[triall]

@amanuensis, oui , théta =90° uniquement pour un point sur le bord de la sphère intérieure . Dans mon dessin plus haut le cercle qui passe par BB' !

[Obamot]

Bonsoir,

Ce qui est le plus troublant, c'est qu'on entend souvent comme explication au magma encore présent dans les entrailles — est qu'hormis les forces qui s'exercent en raions de la rotation de la Terre autour du Soleil — que la cause en serait notamment "les forces gravitationnelles gigantesques en présences et qui exercent une pression/force colossale sur le noyau", or si on considèrait alors (d'une manière ou d'une autre) que:

" les roches qui se trouvent au dessus de nous ne comptent pas "

Cet aspect là tomberait non?

Cordialement.

(voilà, voilà, ça ne se pourrit pas forcément là où s'y attendrait, na!)

[triall]

bonsoir, obamot :

que la cause en serait notamment "les forces gravitationnelles gigantesques en présences et qui exercent une pression/force colossale sur le noyau"

le théorème de Gauss indique que la force s'annule, cela ne veut pas dire qu'il n'y a pas de force .
Un exemple primaire, : 2 gaillards vous pressent contre vos épaules droite et gauche, de manière opposée et symétrique .Vous souffrez , même si au final la somme des forces est nulle .On préfère la situation où il n'y a pas de gaillard du tout et pas de force .
Ceci est pour exprimer qu'un champ nul est différent que pas de champ du tout ! Je me comprends !!

[Dynamix]

L' attraction gravitationnelle que l' atmosphère exerce sur nous est nulle , mais ça ne nous enlève pas la pression atmosphérique due au poids de tout l' air qui se trouve au dessus de nous .
C' est deux choses différentes .
Le magma ne subit pas l' attraction des roches au dessus de lui mais il subit les effets de leur poids .

[Amanuensis]

Cet aspect là tomberait non?

Non. L'intérieur de la Terre n'est pas vide: l'accélération de la gravitation n'y est pas nulle. Les roches au-dessus n'interviennent plus dans le calcul de la gravitation, certes, mais subissent toujours l'attraction de la partie en-dessous. Et donc "écrasent" ce qui est en-dessous. Et comme en plus elles "soutiennent" ce qui est au-dessus, elles en transmettent le poids. D'où une pression qui augmente avec la profondeur, alors que l'accélération de la pesanteur diminue avec la profondeur.