La gravité est nulle à l'intérieur d'une coquille sphérique homogène

[triall]

Votre réaction est étrange... Votre dessin du message #47 est reproduit en fig 1 du pdf de mon dernier message. Que vous faut-il de plus?
Votre devient ridicule, je dois dire...

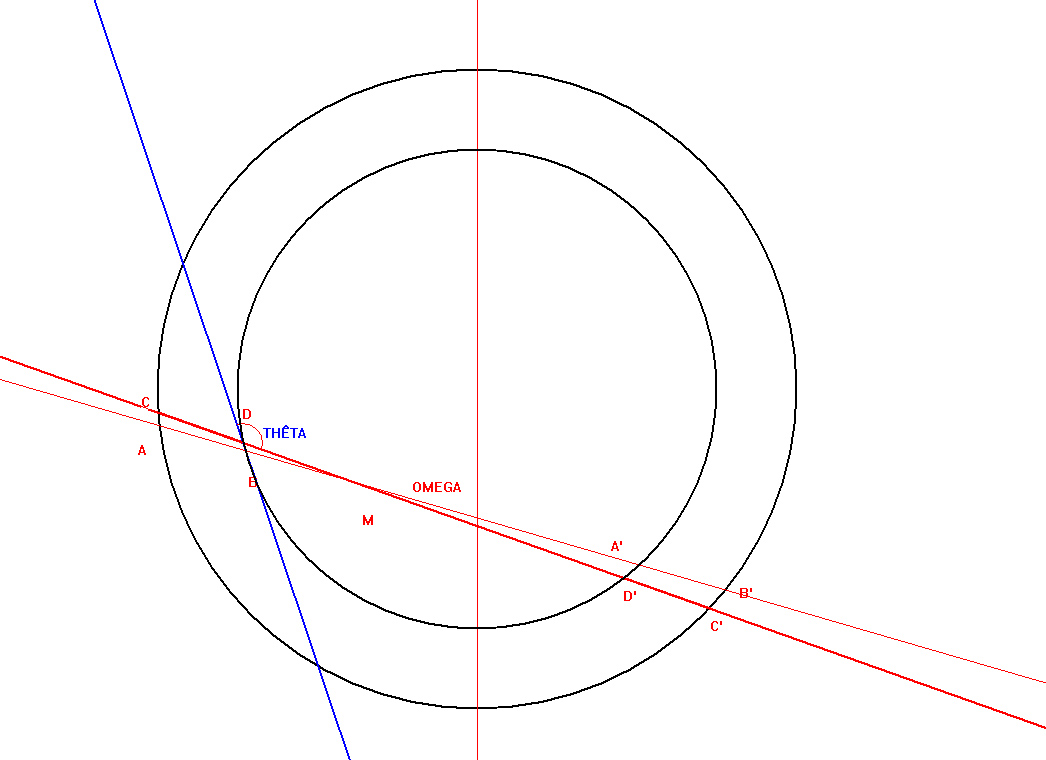
Bonjour, avouez qu 'il fallait aller la chercher cette figure 1 , vers la fin du pdf page 13 , tout de même .En 1 journée, je n'ai pas le temps d'aller voir ; ni personne non plus ! Et si vous allez sur la page 13 de ce pdf , vous constaterez que sur ce dessin, il s'agit d'une sphère , et non d'une coquille !!!
C'est ce que j'essayais d'exprimer , il est très compliqué de répondre à tous le monde correctement , ne devenez pas désagréable , on est là pour apprendre et s'améliorer !
Je crois que vous n'avez pas très bien compris mon "entêtement ". Bien évidement, je ne nie pas la véracité du théorème de Gauss sur la gravité qui serait nulle à l'intérieur d'une coquille sphérique ; j'ai juste prétendu, si vous avez bien suivi , que cette nullité était due à un théorème simple de géométrie qui s'énonce par : " D'un point M quelconque, la distance qui coupe la coquille à gauche AB est égale à A'B' "
J'émettais des réserves quant à la tenue de l'équation vers thêta=0° ou 90° , on ne s'est pas mis d'accord apparemment sur l'origine 0 ou 90.
Avec cette proposition, vraie, donc , me semble t-il , je voulais montrer autre chose sur la force de gravitation, qui est malgré ce que l'on peut dire une vraie force , et donc un échange de quantité de mouvement , ce théorème de Gauss ne le démontre pas, mais donne une raison supplémentaire favorable ..Je ne sais pas si l'on va me laisser le loisir d'aller plus loin , étant donné l'avis très défavorable , majoritairement, de mon post .
Coussin l'a exprimé, il s'agit d'un problème vers la limite quand le point M frôle le cercle intérieur , mais ce n'est pas le problème principal ...
Je voulais exprimer que l 'annulation de la gravité sur une coquille sphérique homogène dépendait de l'égalité AB=A'B' , et de la force en m/d².
Comme je l'indiquais, et coussin aussi , l'expression de la masse vue du point M , donnée par LPFR me pose un problème car il me semble que l'expression de cette masse tend vers l'infini , personne ne m'a donné le terme au numérateur qui tendrait vers 0 ; faisant tendre 0/cos(théta) vers 1 ...merci de me le donner , j'arrêterai mon "entêtement" ,je vous assure , je suis très demandeur d'une formule "correcte" de la masse vue d'un angle oméga et thêta ; et j'essaierai de donner la suite , qui selon moi, est plus intéressante .
Merci de me lire
Bonne journée
A suivre si vous le permettez !
-----

[coussin]

Sitalgo vous a répondu sur ce point: il est suffisant de raisonner sur une sphère d'épaisseur infinitésimale. Pour une coquille d'épaisseur finie, on intègre.

[albanxiii]

Bonjour,

il s'agit d'une sphère , et non d'une coquille !!!

Ce que vous appelez une coquille est appelée sphère en français "scientifique".
Vous confondez sphère et boule ici (tous deux termes mathématiques, et la boule est pleine). En physique on parle de sphère d'épaisseur
Et en plus, dans le pdf de coussin sur la légende on lit "shell".

La discussion commence à tourner en rond sérieusement, là je crois qu'on a fait le tour du sujet et je conseille à ceux qui ne sont pas convaincus de faire l'effort d'un travail de remise à plat personnel (et donc pas sur le forum).

@+

[triall]

Bonjour, donc albanxii ; oui en "français" une sphère est un boule de diamètre a , et une coquille, c'est apparemment la votre de coquille , car une coquille sphérique, selon le "français courant" ou la "géométrie courante" est une sorte de boule de pétanque, possédant un diamètre intérieur et un diamètre extérieur , j 'ai produit des dessins qui montrent que j'ai bien saisi la "nuance entre une sphère (de diamètre unique donc) et une coquille en anglais effectivement shell , avec 2 rayons ou 2 diamètres
Voici une coquille en coupe , j'aimerais , si vous le pouvez, et s'il vous plait ,que vous me donniez la masse des 2 cônes à droite et gauche de M, en montrant, éventuellement que cette masse est proportionnelle à m/d² , prouvant ainsi que la force est égale de part et d'autre du cône , à gauche et droite , démontrant ainsi le théorème de Gauss, qui indique que la gravité est nulle à l'intérieur d'une coquille sphérique .

Bonne soirée .

[Dynamix]

il est suffisant de raisonner sur une sphère d'épaisseur infinitésimale. Pour une coquille d'épaisseur finie, on intègre.

Oui .
LPFR dit :

La masse dm d’une telle surface est égale à où rhô est la densité (absolue !) et ‘e’ l’épaisseur.

C' est assez clair , mais si l' idée d' une "surface pesante" parait étrange on peut remplacer l' épaisseur "e" par une épaisseur "dh" et intégrer .

[LPFR]

Oui .
LPFR dit :

C' est assez clair , mais si l' idée d' une "surface pesante" parait étrange on peut remplacer l' épaisseur "e" par une épaisseur "dh" et intégrer .

Re.
C’est exact. Et quand vous achetez du papier pour votre imprimante vous regardez s’il fait au moins 80 g/m².
A+

[triall]

Bonsoir, je n'arrive pas à copier le message 17 de LPFR ; mais il y a une indication de la masse vue de M qui me chiffonne ; et je n'ai eu aucun justificatif de qui que ce soit ..Par contre on se gausse beaucoup contre moi (humour , rapport au théorème..de Gauss)
dans son message 17 ; lpfr m'indique que

La masse vue par un petit angle solide dOmega autour de la droite vaut :têtha.d.oméga
.l₁²/cos (têtha)
Où thêta est l’angle entre la droite et la surface (90° pour un diamètre et 0 pour une tangente). Sigma, la densité surfacique de masse et l1, la distance du point à la surface.

Sauf erreur de copie
J'ai signalé donc un problème aux alentours de têtha =90° et cos(têtha)= 0 , je n'ai pas eu de réponse satisfaisante, même si l'on s'est bien "gaussé" sur mon ignorance sur la densité surfacique ; et si évidement je sais , au final ce que veut dire un papier d'épaisseur 80g/cm² ; je n'avais pas fait le rapport avec la densité surfacique de masse , personne n'est parfait !...
Je ne vois pas donc , de terme , au numérateur de l'expression têtha.d.oméga
.l₁²/cos (têtha) qui tende vers 0 au numérateur lorsque cos(têtha ) tend , lui vers 0 au dénominateur ?
Bonne soirée

[coussin]

On se gausse parce qu'on vous a déjà répondu. Il y a un cos(theta)^2 au numérateur dans ce que vous notez l1^2.
Je signale quand même que tout cela est expliqué dans le pdf dont j'ai mis le lien...

[coussin]

C'est le message #38.

[triall]

Ouch , alors au final ; L²₁= R²cos(têtha) ; pourquoi Lpfr ne l' a pas enlevé dans son message 17 , c'est "tentant" tout de même de simplifier cos(têtha)²/cos(têtha) par ... cos(têtha) dans une équation !!!Ça évite aussi des problèmes d'infini dans les divisions !
On est d'accord, L₁ est le rayon extérieur le plus grand, et têtha l'angle" indiqué sur le dessin de mon message 64
Arrêtez, s'il vous plait de mettre des liens de 20 pages, ou indiquez, s'il vous plait encore, la page à lire sur ces 20 pages.
Bonne soirée

[inviteb3ad18c6]

bonjour

elle reste en place cette coquille ou pas ? ^^

[Dynamix]

On se gausse parce qu'on vous a déjà répondu.

Pourquoi Gausse ?
Une sphère , c' est Poincaré .

[triall]

Bonjour, ne soyez pas désagréable albanxii ; j’essaie de m’améliorer grâce à cet endroit,ce forum; j’en ai d’autres aussi. Quand je peux j’aide aussi d’autres à comprendre ce qu’il me semble avoir compris .
Ce que je voulais montrer lorsque les élèves de la rangée du fond, près du radiateur auront fini de se gausser ; c’est cette propriété de la gravitation Newtonienne en GmM/d² que l’on voit dans le dessin dessous .
Je passe sur ce qui a été écrit avant car il y a des coquilles de part et d’autre.
MA n’est pas égal , je pense, à Rcos tétha comme a écrit LPFR message 38 , d’ailleurs il n’indique pas ce qu’est R , mais apparemment c’est le rayon d’un des 2 cercles de la coquille, mais de toutes façons ni le grand cercle , ni le petit , il me semble ne convient à R=MA cos(tétha)
Pour voir si dynamix , coussin, albanxii, lpfr suivent , qu’ils m’expliquent cette égalité . R=MA cos(tétha) message 38 , j’aimerais savoir ce qu’est R.
J’ai l’impression que LPFR parle d’un autre dessin ; ou d’une autre démo, où donc apparemment on se passe de l’épaisseur de la coquille en parlant de densité surfacique de masse .je suis preneur , je n’ai pas encore bien compris le principe, puis c’est en anglais scientifique que je ne maîtrise pas.

Passons, pour l’instant, si vous voulez.
Voici le dessin que je propose.

Il s’agit de carrés , bien dans l’axe pour ne pas avoir d ‘angle tétha .
Les volumes obtenus sont des ‘ trapèzes coniques ‘ ; je ne suis pas sûr de l’expression, mais j’ai dessiné 3 volumes, 2 à gauche , et un rouge à droite , tout le monde voit de quels volumes il s’agit.
Ces volumes ont une même épaisseur H ; on sait que l’expression d’un tel volume peut être remplacée par le volume d’un parallélépipède situé à la distance d de M; d étant calculée en prenant le centre de gravité du volume. Ca tombe bien car dans l’expression F= GmM/d² connue où F est la force qui s’exerce mutuellement sur 2 objet de masse m et M ; G étant la constante de gravitation , le centre de gravité est situé à la distance d ..
L’expression du volume de la figure à gauche est donc V=H.A² .
Or on a A/d=A’/d’=constante (Thalès) soit A²/d²=constante , cette constante dépend de l’angle solide …
La masse du volume est rhô.V ; où rhô est la densité de l’objet.
On a alors masse m=rhôHd² x constante . On voit de suite que la masse est fonction directement de d² , et les habitués auront compris que la force F en… 1/d² va être constante le long du cône !
La force sur la masse-test M de masse M est alors égale à F=G. x rhôHd² x constante x M /d²=Gx rhô x H x M xconstante force qui donc ne dépend pas de m , le d² /d² faisant 1 ….et qui est constante dans la mesure ou l’épaisseur H est constante , que l’angle solide est le même que rhô soit le même G de même , et la masse test M identique aussi !
Pour résumer tous les volumes dessinés sur mon dessin exercent une force d’attraction égale sur M la masse test ..
Si donc on avait de part et d’autre de cette masse test 2 volumes comme le rouge et le bleu, uniquement , le champ de gravité serait nul au point M !
Je « vois » dans la coquille sphérique à peu près le même « environnement » sauf qu’il s’agit de vrais cônes « ronds » et de vrais angles solides ronds aussi , et la démonstration est plus compliquée, c’est l’angle tétha qui me pose problème !
A suivre s’il vous plait .
Bonne journée.

[LPFR]

Re .
Aussi longtemps que vous vous entêterez à travailler avec des parallélépipédiques de dimensions non infinitésimales, vous n’avancerez pas d’un pouce.
Je pense que vous devriez essayer de comprendre ce qu’est un angle solide.

Et si les réponses que je vous ai données au début étaient sommaires, c’était parce que vous avez rédigé votre intervention comme un défit pour que nous trouvions la "découverte" que vous veniez de faire sur la propriété géométrique fondamentale qui expliquait la gravité nulle. Vous n’avez pas rédigé ça comme une question à laquelle vous ne saviez pas répondre.

Maintenant on constate que non seulement vous n’avez pas compris le problème, mais que vous refusez d’accepter le solutions que l’on vous donne, soit parce que l’article est trop long, soit parce que on utilise de angles solides infinitésimaux, ou parce que vous ne comprenez pas les démonstrations que l’on vous donne.

Pour ma part, j’ai dit ce que j’avais à dire et je n’irai pas plus loin. Je ne sais pas faire mieux.

A+

[triall]

@lpfr ; j'ai laissé tomber la coquille sphérique; pour l'instant , c'est vrai que j'ai de la difficulté à travailler avec les angles infinitésimaux ; mais pour ma part, avec ma notation j'aurais dm=d(oméga) .(cos(90-tétha)MB)² .AB.rhô ensuite l’expression de la force de Newton me pose problème car on aurait Gdm.M/L² avec L distance de M au centre de gravité de ABCD et L n'est pas MB , si on admet que MB=L c'est bon, car on aurait l'expression de la force F=Gd(oméga) .(cos(90-tétha))² .AB.rhô comme AB , selon "ma" question primitive est égale à droite et gauche de M que rhô et oméga sont aussi identiques à droite et gauche de M; l'expression de la force est la même à droite et gauche . Le champ de gravité s'annule au point M .C'est votre Rcos (tétha) ; je n'ai pas saisi ce R ....
Le fait que l'on se passe de l 'épaisseur de la coquille me chagrine, car "mon" égalité primitive AB=A'B' et CD=C'D' n'entrait pas en jeu .

Je suis passé à autre chose; mon dernier dessin n'a pas besoin de notation infinitésimale, ce sont de "vrais" volumes, et je voulais montrer une propriété de la gravitation, cette égalité des forces pour ces volumes suggère qu'il existe un flux , et que le fait important, en fait pour annuler la gravité était la distance traversée par une particule venue de l'extérieur ; étant donné que comme l'univers est isotrope, en moyenne pour chaque particule venant de la gauche , il en existerait une venant de la droite, exactement à l'opposé ....C'était le but de mon dernier dessin message 73 .
Avec ce principe, la démonstration du théorème de Gauss sur une coquille sphérique est évident, vue l'égalité AB=A'B' et CD=C'D' ....la démonstration précédente tombe de suite, aussi vu l'épaisseur identique H ....
Cette façon de concevoir la gravitation a été décrite par Nicolas Fatio de Duillier et Lesage Louis Georges né en 1724 , elle est à connaître, je crois.

[Dynamix]

Question que je me pose depuis le début :
Pourquoi une sphère ? C' est très restrictif .
Pourquoi pas un cube ou une patatoïde ?
Evidemment le coups de la propriété triviale d' une droite qui coupe la surface tombe à l' eau .

[sitalgo]

C'est votre Rcos (tétha) ; je n'ai pas saisi ce R ....

Vite fait alors. LPFR a pris l'exemple de M situé au milieu, dans ce cas AM = R cos theta.
Si M n'est pas au milieu, la formule sera plus compliquée mais sera toujours fonction de cos theta.
Et on aura cos²/cos, ce qui tend vers 0 et non l'infini.

[triall]

Merci sitalgo pour cette réponse , mais c'est ce que je n'ai pas compris, si M est au milieu, les masses à droite et gauche sont égales , la force aussi , il n' y a pas besoin de démonstration puisque on a AB=A'B' et CD=C'D' .J'ai fait exprès un dessin message 45 avec M au milieu , on voit clairement que les masses ABCD d'une part et A'B'C'D' d'autre part sont égales !Si M est placé au centre c'est encore plus évident !

J'avoue que je n'ai pas lue la démonstration de Newton, ni celle de Gauss , sur les liens que l'on m'a indiqué je ne vois qu'une sphère(1 seul rayon hein ?) et pas de coquille sphérique (2 rayons, comme sur mes dessins) ! Je le ferai un autre jour, si je la trouve en français , ça m'aidera beaucoup !
Je pense avoir trouvé une expression de dm qui va bien , mon angle solide oméga coupe ma coquille avec une sorte d'ellipse en 2 endroits, une petite , plus proche de M(qui n'est plus au milieu hein ?) et une plus grande , j'ai donc 2 surfaces dS₁ et dS₂pour avoir dS plus précisément je calcule la surface de cette ellipse en prenant l'ellipse entre les 2 ce qui fait (dS₁ +dS₂ )/2 et donc la distance à M de cette ellipse est (MA+MB)/2 , exactement la distance de M au centre de gravité de ABCD , qui entre en jeu dans l'expression de la force donnant au final une force égale aux 2 cônes situés de part et d'autre de M ..mais c'est un peu du bricolage ...
Bonne soirée.

[Amanuensis]

Question que je me pose depuis le début :
Pourquoi une sphère ? C' est très restrictif .
Pourquoi pas un cube ou une patatoïde ?

Il me semble que la sphère est le seul cas de surface fermée de masse surfacique constante induisant une accélération de gravitation nulle en tout point de son intérieur.

Même en faisant sauter la condition de masse surfacique constante je me demande s'il y a d'autres solutions?

[triall]

Bonjour, sur une patatoïde , la gravité est nulle .....au centre de gravité , non ?

[albanxiii]

Bonjour,

Bonjour, ne soyez pas désagréable albanxii ; j’essaie de m’améliorer grâce à cet endroit,ce forum; j’en ai d’autres aussi.

Ne me donnez pas d'ordre triall.
Je vous dis juste qu'on a fait le tour de vos questions et que vous tournez en rond. Cela ne sert à rien de poster et reposter sans cesse toujours les mêmes choses auxquelles on a déjà répondu en long, en large et en travers.

@+

[triall]

Bonjour albanxii , je réponds à amanuensis et dynamix .
Si je poste c'est que j'ai soit , encore des explications à demander , ou à livrer !
Je voulais signaler sur mon message 73 que selon la gravité de Lesage, l'égalité des segments AB=A'B' et CD=C'D' à elle seule explique l'annulation de la gravité à l'intérieur d'une coquille sphérique, d'une façon étonnante de simplicité , il me semble que c'est très très intéressant et bien entendu tout à fait dans le sujet .
C'est toujours intéressant de noter qu'il y a des solutions géométriques très rapides .
Mais si cela n'intéresse personne tant pis !
Bonne journée .

[Dynamix]

Il me semble que la sphère est le seul cas de surface fermée de masse surfacique constante induisant une accélération de gravitation nulle en tout point de son intérieur.

Après mûre réflexions , il me semble aussi sans pouvoir le démontrer .
Par contre , je me demande si pour certaine formes il n' y aurait pas plusieurs de points de gravité nul , voir même une ligne .


@Triall , je parle de corps creux .

[Amanuensis]

Par contre , je me demande si pour certaine formes il n' y aurait pas plusieurs de points de gravité nul , voir même une ligne .

Je n'ai même pas d'idée ou de piste pour deux points!

Des lumières sur ce point?

[LPFR]

Re.
L'axe d'un tuyau.
A+

[Dynamix]

De longueur infinie .

[triall]

J'ai comme l'impression que la gravité est nulle aussi à l'intérieur d'un tuyau(pas que sur l'axe) !

[Amanuensis]

De longueur infinie .

Je confirme l'objection: "de surface fermée de masse surfacique constante" dans mon message #79

[triall]

Oui, je confirme, je suis certain maintenant que la gravité est nulle aussi à l'intérieur d' un tuyau creux, homogène et infini .
Pour que ce soit le cas, il suffit que toutes les droites passant par un point quelconque (intérieur à l'objet) coupe l'objet de part et d'autre sur 2 distances égales , le but de ce post était pour moi de montrer ce "théorème" (message 73 ...) .
Pour un tuyau fini, vers le bord, ce n'est pas le cas , une droite d'un côté peut ne pas couper le tuyau , et le couper de l'autre , mais oui pour un tuyau infini !

[sitalgo]

Ce qui est important est qu'il y ait une dimension infinie, peut importe que la section soit fermée ou ouverte, il y aura toujours un axe de gravitation nulle. Au plus simple, une surface plane.
L'axe de gravitation nulle pouvant être à l'extérieur d'une section fermée.