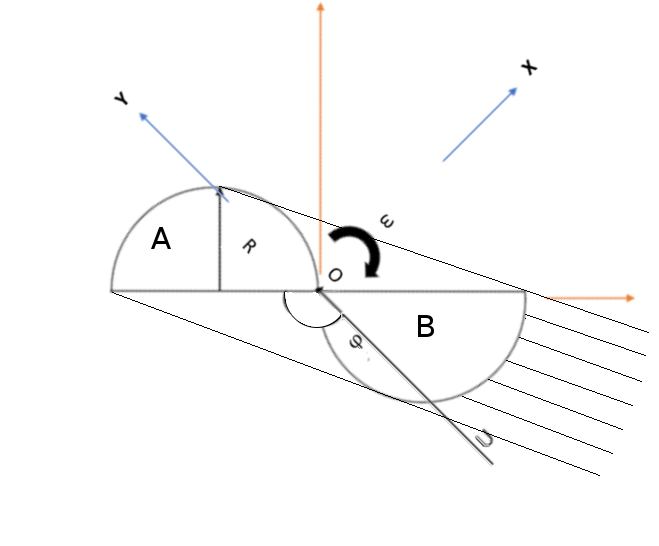
C'est la pâle entrante qui est la source principale de poussée, tandis que la pale sortante elle crée plutôt un freinage non ?Pour la pâle sortante, qui est la source principale de poussée
Je ne suis pas sûr de bien comprendre où se situe le problème pour le coup. Le fait que C"x -> C'x n'est justement pas pris en compte par le fait que l'intégrale a été scindée en deux partie, et le résultat multiplié par 2 à la fin ?
La pâle entrante est celle qui pénètre le vent. Elle cause un freinage mais a un bon profil donc la traînée est faible.
La pâle sortante est celle qui suit le vent. Elle agit comme une voile. Elle provoque la rotation.
Si la pâle sortante a une vitesse linéaire supérieure à celle du vent, le vent ne peut plus la pousser !
Au départ, le vente la pousse, elle tourne lentement, U sin (phi) > wR et la vitesse relative est dans le sens du vent.
Mais elle va accélérer. Là où U sin(phi) = wR, la pâle est immobile dans le vent. Il n'y a plus de traînée.
Si U sin(phi) < w.R ... la pâle tourne plus vite que le vent. Il n'y a plus de poussée mais uniquement du freinage.
Le problème c'est que cela dépend de phi... Et cela apparaît dès les premiers instants...
Dernière modification par Nekama ; 26/05/2020 à 13h29.
Petite erreur de compréhension de ma part sur pâle entrante/sortante, j'ai corrigé ça.
Pour la pale sortante on a écrit U sin(phi) + wR, est-ce qu'il y a une erreur de signe et cela devrait être un signe moins pour la composition des vitesses ? Si c'est une erreur de ma part alors je comprends le problème...
Ou alors il manque un effort de trainée qui lui a bel et bien tendance à freiner la pâle sortante, l'effort serait Fx = - 0.5rhoSC"'xV² Y' avec V = Wr et C"'x serait à considérer pour la partie "bombée" du demi-tube.
Pour la pale sortante, la vitesse de rotation et la vitesse du vent vont dans le même sens.
On a donc bien une vitesse relative v = U sin(phi) - wR.
Selon le sens de la vitesse on a :
v > 0 : une poussée avec une traînée dans le sens du vent qui a tendance à pousser la pâle
v < 0 : une traînée de freinage dans le sens opposé à la rotation et qui a tendance à freiner la pâle.
Ok donc c'est une erreur de ma part, je pensais que puisque les vitesses agissent dans le même sens on les sommait simplement. Dans ce cas, et pour ne pas reproduire la même erreur qu'avant, la vitesse relative de la pale entrante est bien de v = U sin(phi) + wR ?Pour la pale sortante, la vitesse de rotation et la vitesse du vent vont dans le même sens.
On a donc bien une vitesse relative v = U sin(phi) - wR.
Ce cas là est un cas limite non ? Physiquement j'ai du mal à voir à quel moment la vitesse de rotation deviendrait supérieure à celle du vent, et comment le prendre en compte dans les équations.v < 0 : une traînée de freinage dans le sens opposé à la rotation et qui a tendance à freiner la pâle.
L'effort de trainée que j'ai expliqué au dessus serait-il alors à prendre en compte ?
Oui, pour la pâle entrante, c'est U sin(phi) + w.R
Hélas non ce n'est pas un cas limite à cause du sin(phi) qui peut être très faible.
Plus w va augmenter et plus on va assister au phénomène dans la zone phi = [0 ; a* [ et ]a* ; pi] de la pâle entrante.
Par contre le cas ou a* = 90° est un cas limite
Il n'est cependant pas théoriquement inaccessible à cause de la portance qui reste tout le temps positive quant à elle.
----
On va aboutir.
Il faut intégrer en scindant l'intervalle avec a*
La vitesse de rotation limite sera celle pour laquelle on a un moment moteur moyen = moment de freinage moyen.
Ensuite, on compare avec des données expérimentales.
Tout cela est un peu flou pour moi.
Même si le terme U sin(phi) - w.R peut effectivement être négatif, en quoi cela pose-t-il problème puisque la vitesse est élevée au carré ?
Et du coup, à quoi correspond a*, un angle limite pour phi qu'il faudrait déterminer expérimentalement ?
De manière générale : une force de traînée va dans le même sens que celui de la vitesse relative.Envoyé par cmole
Et donc, si la vitesse relative est > 0 ou < 0, la force est > 0 ou < 0.
Dans nos calculs, on l'a toujours considérée comme > 0 ( à cause du v^2 justement )
a* ne se détermine pas expérimentalement. Ce sera un paramètre dans le calcul de l'intégrale.Et du coup, à quoi correspond a*, un angle limite pour phi qu'il faudrait déterminer expérimentalement ?
Il faut intégrer de :
1/ 0 à a*, et, pi - a* à pi pour déterminer la moment de freinage
2/ de a* à pi - a* pour déterminer la moment de poussée
---
Ce n'est pas a* qu'il faut déterminer expérimentalement.
Ce qu'il faudra faire quand l'intégrale sera correcte, c'est rassembler des données d'internet pour comparer les résultats de la formule finale avec des mesures.
Ah oui d'accord, je comprends mieux. En relisant le document sur les anémomètres que j'avais partagé j'ai remarqué que pour éviter cette approximation ils utilisaient un vecteur (U-Rw)/(|U-Rw|), ce qui est plus rigoureux.De manière générale : une force de traînée va dans le même sens que celui de la vitesse relative.
Dans ce cas, comment fixer ce paramètre ? J'avoue avoir du mal à en saisir l'intérêt. Même si je comprends bien le problème lié à U sin(phi) - wR je ne vois pas en quoi ce paramètre permet de le contourner.a* ne se détermine pas expérimentalement. Ce sera un paramètre dans le calcul de l'intégrale.
C'est purement mathématique. On ne sait pas calculer un intégrale avec une valeur absolue. Il faut s'en débarrasser.
- Il est indispensable de scinder l'intervalle d'intégration à cause de la valeur absolue qui n'est pas intégrable.
- Comme on ne sait pas où elle change de signe, il faut bien introduire un paramètre inconnu : a* (ou un autre nom)
En a*, on a v = 0
En phi < a* et phi > pi - a* : |v| = w.R - U sin(phi)
En phi > a* et phi < pi - a* : |v| = U sin(phi) - w.R
a* est l'angle à partir duquel, on passe d'un traînée accélératrice à une traînée de freinage et a* dépend de w.
Il faudra donc trouver pour quel a* on a un moment nul.
Je pense que je commence à comprendre ce phénomène même s'il n'est pas du tout intuitif. Je vais essayer de faire un résumé de ce que j'ai compris, pour voir si je ne pars pas dans la mauvaise direction.
Pour la pale sortante on a une vitesse relative V = |U sin(phi) - w.R|. Le problème est que la force de trainée induite par cette vitesse dépend de la direction de ce vent relatif, donc du signe de U sin(phi) - w.R et par conséquence de l'angle phi.
- dans le cas où U sin(phi) - w.R > 0 alors on a bien un moment de poussée qui a tendance à mettre en rotation le système. On a alors F = 0.5rhoSCx(U sin(phi) - w.R)² Y' (avec les notations de la note de calcul écrite jusque là).
- dans le cas où U sin(phi) - w.R < 0 alors on a un moment de "freinage" qui a tendance à stopper la rotation. On a alors F = - 0.5rhoSC'x(w.R - U sin(phi))² Y'.
Pour prendre en compte ce phénomène on introduit un paramètre a* qui traduit ce changement de signe de la vitesse relative. C'est là que ça s'mebrouille (oui encore un peu plus) puisque je ne comprends pas comment on scinde l'intégrale. J'aurais intuitivement scindé en : [0;a*[ pour le moment de freinage, et ]a*;pi] pour le moment de poussée.
a* étant un angle qu'il faut déterminer et qui est caractérisé par un moment nul.
Tout cela est-il correct ?
Est-ce que ce phénomène a réellement lieu physiquement ou il s'agit simplement d'une limite de l'hypothèse où on sépare les vents en deux composantes ?
Et, dernière question, on ne prend pas en compte de trainée liée à la pale sortante selon -Y', est-ce une hypothèse acceptable ou un simple oubli ? j'aurais tendance à écrire cet effort comme cela : Fx = -0.5rhoSC'xwR² Y'.
Encore merci pour votre aide !
ok pour ce qui précède.
si l'équation :Pour prendre en compte ce phénomène on introduit un paramètre a* qui traduit ce changement de signe de la vitesse relative. C'est là que ça s'mebrouille (oui encore un peu plus
a* étant un angle qu'il faut déterminer et qui est caractérisé par un moment nul.
w.R - U Sin(phi) = 0
çad
sin(phi) = W.R/U
a pour solution phi = a*, elle alors également pour solution phi = pi-a*
Le signe change donc en a* et en pi-a*
pas juste en a*
C'est bien lié au problème général du rotor quand on prend en compte la vitesse relative du rotor.Est-ce que ce phénomène a réellement lieu physiquement ou il s'agit simplement d'une limite de l'hypothèse où on sépare les vents en deux composantes ?
Ce n'est pas lié à la séparation.
Pour la pale sortante, le vent et la vitesse de la pale sont dans des sens opposés. C'est donc toujours un freinage.Et, dernière question, on ne prend pas en compte de trainée liée à la pale sortante selon -Y', est-ce une hypothèse acceptable ou un simple oubli ? j'aurais tendance à écrire cet effort comme cela : Fx = -0.5rhoSC'xwR² Y'.
Encore merci pour votre aide !
Pour la pale rentrante, ils sont en "compétition". Selon celui qui est le plus grand, on aura poussée ou freinage.
C'est beaucoup plus clair, je pense que j'ai saisi cette subtilité alors merci !
J'ai remis à jour le PDF qui reprend toutes ces réflexions, en écrivant l'intégrale "finale" qu'il restera à résoudre. ROTOR SAVONIUS.pdf
Cela vous semble-t-il correct maintenant ? J'ai essayé d'expliquer au mieux l'introduction de l'angle a*, mais pas si simple d'expliquer ce qu'on vient à peine de comprendre. Si tout cela est correct, je m'attaquerai à la résolution de cette intégrale (pas bien méchante, mais assez conséquente quand même !).
ca me semble bon.
Super ! Je me m'attelle à la résolution de l'intégration dès demain pour vous montrer les résultats.ca me semble bon.
Bonjour, je reviens vers vous avec le résultat du calcul ! Seulement celui-ci ne me convient pas puisqu'il y a un terme non factorisable par (Cx'-Cx) ou par (Cx'+Cx). De plus ce terme, dépendant de Cx', aurait tendance à faire tourner le système avec son signe -. Il y a donc nécessairement une erreur, mais je n'arrive pas à la retrouver et ça fait plusieurs heures que je sèche...
Voici le PDF, j'ai essayé de détailler le calcul autant que possible sans trop alourdir. ROTOR SAVONIUS.pdf
Merci aux courageux qui se lanceront dans les calculs !
Bonjour, après quelques jours j'ai relu et refait les calculs en trouvant toujours le même résultat. Je me pose donc la question si le fait de pouvoir factoriser tous les termes par (Cx'-Cx) et (Cx'+Cx) est quelque chose de "nécessaire" ou une pure intuition. Même si je comprends bien que les deux pales ont des actions antagonistes, je me demande s'il n'est pas logique finalement de trouver un terme dépendant uniquement de Cx' puisque les deux pales créent bien un effort qui a tendance à freiner le rotor à cause de sa propre vitesse de rotation.
J'avoue avoir un peu de mal à analyser ce résultat plutôt calculatoire (manque d'expérience, j'imagine), un avis serait m'aiderait grandement !
Bonjour,
Cette approche considérant le repère propre de l'éolienne en rotation est une approche intéressante.
Cependant, il me semble qu'il est nécessaire de considérer les C'x et C'z comme des paramètres variables et non pas comme des constantes.
En effet avec le vent de face, le C'x est réellement le Cx d'un demi-tube convexe mais avec le vent (relatif) de travers, C'x = Cz coefficient de portance du demi-tube.
de même par vent arrière, le C'x devient le Cx d'un demi-tube concave (là je n'ai pas compris l'intérêt d'introduire un C''x).
Ou alors, quelque chose m'échappe dans cette modélisation.
Dernière modification par DidierGr ; 04/06/2020 à 12h09.
Bonjour
L'intérêt de décomposer le vent selon le repère tournant permet justement de considérer (en première approche) des coefficients Cx, Cz,... constants. D'une certaine façon c'est le vent qui "est tournant" et le rotor "fixe". Cette hypothèse permet (sans l'erreur qui traine dans le PDF) de résoudre l'intégrale qui donne le couple du rotor pour un vent incident donné. Sans cette méthode, les coefficients dépendent alors de l'angle phi et il serait impossible (sauf grosses hypothèses énoncées dans les messages précédents) de résoudre l'intégrale finale.
Bien sûr, une fois le résultat final obtenu (bientôt on espère !) il faudra recroiser les résultats avec ceux expérimentaux trouvables sur internet.
Salut Cmole,
J'avais perdu le fil de vue...
Je n'ai pas le temps de vérifier les résultats des calculs, sorry...
Mais il est naturel de s'attendre à ce qu'il y ait des termes C'x - Cx et C'x + Cx vu qu'on a des sommes et des différences au carré.
Il faut laisser reposer tout, faire un autre petit truc, et relire tes calculs dans quelques jours
Bonjour,
Pas de soucis, je comprends tout à fait ! Je vais effectivement prendre quelques jours pour laisser reposer tout ça et reprendre/relire les calculs proprement. Une fois le bon résultat trouvé (on reste positif
Encore merci pour toute l'aide apportée !
Bonjour,
D'un point de vue analytique et en prenant en compte le repère R1 (x',y',z') je considère:
1) Le vent vitesse Vv qui s'oppose au mouvement (Cx') et est uniquement fonction de la vitesse de rotation du demi-cylindre.
Il peut être considéré en vitesse instantanée et intégré ou en vitesse moyenne sur 1 tour.
Il peut être facilement simulé en soufflerie par mesure du couple agissant en statique sur le demi-cylindre avec un vent de face.
2) Un vent vitesse radial est probablement à prendre en compte du fait de la rotation, il devrait avoir un effet positif sur la portance.
3) la composante en y' du vent U (sinusoïdale alternative agissant via le Cx et Cx' du mobile)
4) la composante en x' du vent U (cosinusoïdale alternative agissant via le Cz à gauche puis à droite du mobile)
5) le masquage d'un demi-cylindre par l'autre quand la composante en x' du vent U est à droite et annulant la portance alors qu'elle pourrait être quasi maximale.
6) l'écoulement du vent suivant l'axe z=z' agissant comme une force sur l'axe z.
J'en oublie peut-être mais le point qui me semble le plus important à considérer est le point 5 sauf à reconsidérer le modèle avec un seul demi-cylindre en rotation au lieu de 2.
Il est possible de réaliser cette forme avec une hélice suivant l'axe z.
Autre possibilité, déplacer les angles de masquage avec 3 demi-cylindres.
Personnellement, j'opterai pour une décomposition du modèle théorique suivant ces différents points avant d'en faire une addition vectorielle.
Sur les points que j'ai oublié, l'effet Magnus sur les demi-cylindres est aussi à prendre en considération.
Pas simple la mécanique des fluides ... le souvenir que j'en ai au cours de mes études, c'était des intégrales triples exactes mais impossibles à résoudre suivi de simplifications qui permettaient d'obtenir des résultats avec des marges d'erreur de l'ordre de 20% !!!
Bonjour DidierGr, merci pour votre intervention ! J'ai plusieurs questions à propos de vos remarques.
Si j'ai bien compris chacun de vos points, les remarques 1, 2, 3 et 4 ont bien été prises en compte dans le PDF que j'ai envoyé, c'est bien ça ?
En revanche, je ne comprends pas très bien ce que vous voulez dire avec les points 5 et 6, ni comment les faire intervenir sous forme d'équations. Pour l'effet Magnus c'est simple, je n'en connaissais même pas l'existence
Merci de l'aide que vous apportez, j'espère arriver à un résultat satisfaisant !
Je ne peux plus éditer le message, mais j'ai en fait d'autres questions.
Dans l'étude menée jusque là (visible dans le PDF) on considère que chaque pale voit une vitesse tangeantielle relative de ±((Usin(φ) - ωR)Y' pour la pale sortante, et (Usin(φ) + ωR) 𝑌′ pour la pale entrante. Seulement, je ne comprends pas bien pourquoi on ne scinde pas les efforts selon Y' de la manière suivante :
Pour la pale entrante un effort de trainée responsable de la rotation F = 0.5rhoSCxUsin(φ)²Y ' et un effort de trainée freinant la rotation F = -0.5rhoSCx'w²R² Y'.
Or dans le PDF on a utilisé une composition des vitesses pour avoir un seul effort par pale dans la direction Y', soit F = ±0.5ρSxCx²(Usin(φ) - ωR)² 𝑌'. Pourquoi choisir cette méthode là, et pas la première ? Il doit y avoir une subtilité mais je ne saisis pas...
Bonjour cmole,
Oui, les points 1 à 4 sont pris en compte mais il me semble qu'il serait plus clair de bien en séparer les composantes.
Pour le point 5, cela revient à considérer un vent nul (au lieu du vent U) lorsqu'une pale masque l'autre suivant un secteur d'angle à déterminer géométriquement.
Le point 6 est plus délicat et dépend de la géométrie en z du rotor (fermé en bas et ouvert en haut => écoulement vers le haut => force vers le bas) les actions en x et y ne sont pas évidentes à modéliser mais l'action résultante serait probablement différente si le haut du rotor était fermé. Il est peut-être possible de considérer une perte d'une partie du flux du vent U.
Pour l'effet Magnus : https://fr.wikipedia.org/wiki/Effet_Magnus il est la conséquence de la rotation de l'ensemble dans le flux de vent U
Dernière modification par DidierGr ; 13/06/2020 à 11h19.
Bonjour DidierGr,
Effectivement, cela manque de clareté et je vais essayer de séparer les composantes pour mieux expliquer les résultats.
Je ne suis pas sûr de bien comprendre, les pâles ne sont pas censées se masquer comme on peut le voir sur le schéma paramétré (ou alors je rate quelque chose !).Pour le point 5, cela revient à considérer un vent nul (au lieu du vent U) lorsqu'une pale masque l'autre suivant un secteur d'angle à déterminer géométriquement.
Si j'ai bien compris, les points 6 et l'effet Magnus n'ont pas d'influence directe sur la vitesse de rotation du système mais sont des composantes à prendre en compte pour dimensionner le rotor c'est bien ça ?
Le point 6 a une résultant selon l'axe Z, aucun moment n'est créé par cette force mais il serait judicieux de le calculer pour choisir, par exemple, les roulements adaptés.
L'effet Magnus (pour le coup je suis moins sûr de moi, je suis en terre inconnue
Sinon, suivant les conseils de Nekama, j'ai repris tous les calculs depuis le début et je retombe exactement sur le même résultat. Pensez-vous qu'il est cohérent ? On avait parlé du fait que les pâles ont des actions symétriques et antagonistes et donc que les termes devaient être factorisables par (Cx'-Cx) et (Cx'+Cx) seulement ici j'ai un terme dépendant uniquement de Cx', et je ne sais pas comment l'interpréter...
Je rejoins le fichier. ROTOR SAVONIUS.pdf
Merci pour votre aide !
Bonjour
Je reviens vers vous avant même vos réponses aux différentes questions : j'ai (enfin !) trouvé l'erreur de calcul qui trainait dans le PDF. L'erreur est toute bête, j'ai intégré la pale sortante sur [pi, 2pi] alors qu'il fallait intégrer sur [0, pi]. Ca semble logique dit comme ça, mais cela m'aura bien fait réflechir !
Maintenant il ne reste "plus qu'à" trouver une relation liant a* à la vitesse de rotation et comparer les résultats à ceux expérimentaux (en ne perdant pas de vue qu'on n'a pas d'espacement entre les pales, il devrait donc y avoir un rendement plus faible).
ROTOR SAVONIUS.pdf Voilà donc le PDF corrigé ! Avec vos remarques il faudra que j'explique plus clairement les efforts présents, mais chaque chose en son temps.
Merci pour votre aide !
Bonjour,
Je vais lire avec attention votre document.
Concernant le masquage du vent par l'autre demi-tube, voici une illustration reprenant votre schéma.
La zone hachurée en bas à droite représente le flux d'air arrivant sur le demi-tube B et totalement masqué pour A (U=0)
De fait, il serait aussi nécessaire de considérer une zone plus large où le vent arrivant sur A est masqué en partie, sur le schéma, une partie du demi-cercle de B masque le vent U vers A.
Cet effet de masquage a donc une incidence importante sur l'efficacité du rotor.
Ce qui mène à considérer en première approche, un flux de vent tournant sinusoïdal régulier pour chaque demi-tube et lui soustraire le flux de vent masqué par l'autre demi-tube (en partie ou en totalité suivant l'angle phi).
Oui en effet mais le point 6 a aussi un effet de déviation sur le flux du vent qui aura tendance à s'orienter en partie suivant l'axe z, il en résulte donc une diminution de la composante horizontale de U.Si j'ai bien compris, les points 6 et l'effet Magnus n'ont pas d'influence directe sur la vitesse de rotation du système mais sont des composantes à prendre en compte pour dimensionner le rotor c'est bien ça ?
