Bonjour à tous
Première intervention sur le forum, j'espère ne pas me tromper de section et si c'est le cas veuillez m'excuser.
Je m'intéresse actuellement au rotor de Savonius et je cherche à savoir s'il est possible de prédire ses performances.
Je cherche donc à déterminer le couple créé par le vent sur le système, et la vitesse de rotation du rotor pour une vitesse de vent donnée. Je ne sais pas grand chose sur ce type d'éolienne, c'est pourquoi je demande votre aide.
Détermination du couple :
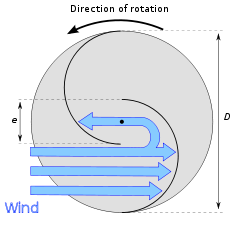
Le couple est créé à partir de la différence d'effort de trainée entre les hémisphères concave et convexe du rotor. Si, dans un premier temps, on prend l'espacement e = 0 on a alors Ctot= Cconcave - Cconvexe avec C = 0,5ρSCxV². Seulement, je suppose que le coefficient de trainée de chaque hémisphère varie avec la rotation du rotor, et là je ne sais absolument pas comment l'estimer convenablement. Dans le cas où le vent vient "frapper" les hémisphères de face on peut se débrouiller, seulement dès que le rotor se met à tourner je ne sais pas comment estimer Cx en fonction de l'angle créé avec le vent (d'ailleurs S varie aussi, mais là c'est plus simple à estimer).
Enfin et pour en terminer avec le couple, est-il possible de faire intervenir l'espacement e dans le calcul du couple ?
Détermination de la vitesse de rotation :
Pour estimer la vitesse de rotation du rotor avec une vitesse de vent donnée j'ai pensé à utiliser (peut être un peu naïvement ?) le PFD, on a alors :
Ctot - Cresistant = Jθ (où θ est l'accélération angulaire).
Le couple résistant peut être estimé assez facilement avec le calculateur en ligne de SKF et J avec un logiciel de CAO. Une fois ces paramètres connus on a une équation différentielle qu'il "suffit" de résoudre pour obtenir la position, la vitesse, l'accélération.
Seulement pour appliquer cette méthode j'ai besoin de connaître le couple, et on en revient au point précédent !
Est-ce que cette méthode semble correcte quand même ?
J'espère que je trouverai des réponses car malheureusement je n'ai rien trouvé de concluant après mes nombreuses recherches. Merci à ceux qui prendront le temps de m'aider, et bonne journée !
-----





 .
.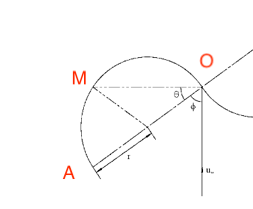
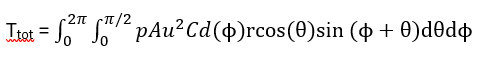 qu'il n'est pas possible de résoudre à moins de connaître Cd(ϕ).
qu'il n'est pas possible de résoudre à moins de connaître Cd(ϕ).