Coordonnées de Painlevé : lecture et translation

[Mailou75]

Bonjour,

Le but est ici de mieux comprendre la signification des coordonnées de Painlevé et d'en proposer une translation horizontale redressant une trajectoire de chute libre depuis l'infini, que j'ai nommée Slide.

Ces dernières présentent une analogie avec les coordonnées de Lemaître (voir exemple ici https://forums.futura-sciences.com/a...ml#post5909753) dans le sens où la trajectoire se trouve être verticale (axe des ordonnées). Elles présentent des avantages, comme le fait que l'horizontale soit l'espace du voyageur et un inconvénient majeur : elles ne valent que pour une seule trajectoire !

Painlevé

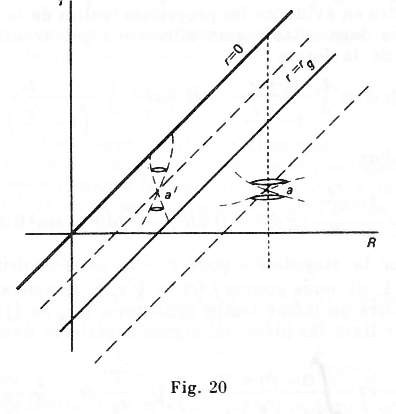
Les voyageurs (Rouge et Bleus) représentés ont été choisis de telle façon à ce qu'ils croisent des immobiles (Verts) à intervalle de temps propres régulier. Ainsi, un voyageur qui déclencherait son chronomètre à 2,826Rs passerait l'horizon à exactement 2,5s (secondes pour un trou noir de rayon 300.000km en réalité l'unité de temps est Rs/c). En jaune on voit le cône passé et en violet l'espace des immobiles, ce qui serait une horizontale en coordonnées de Schwarzschild.

A titre d'exemple, quand Rouge croise le stationnaire Vert à 1,842Rs son chrono indique T=1,5s et cet évènement est pris comme date de référence pour l'observateur éloigné t. Les autres croisements auront eu lieu a une date ultérieure t-...

La particularité de ces diagrammes c'est qu'ils montrent des surfaces d'espace-temps locales, cad des "carrés" de 0,1Rs par 0,1s. Carrés locaux, dans le sens où pour eux tout est normal dans leur référentiel, mais déformés quand ils sont représentés d'un autre point de vue. Les losanges des voyageurs ont une base de 0,1Rs et une hauteur de 0,1s, leur angle est donné par la vitesse de chute locale (par rapport aux immobiles). La vitesse de chute est la formule de Newton dr/dT=c*racine(Rs/r).

Si on note (z+1) le redshift auquel l'observateur éloigné perçoit les immobiles alors les immobiles ont pour base 1/(z+1) et pour hauteur (z+1) exactement comme ils seraient représentés en coordonnées de Schwarzschild, cad vus par l'observateur éloigné : compressés radialement et étirés dans le temps (redshiftés). Cette fois leur angle est donné par la courbe de l'espace, qu'on comprendra mieux plus tard...

Slide

On fait glisser horizontalement tout le graphe de façon à ce que Rouge ait une trajectoire verticale. Ainsi les carrés d'espace temps de Rouge sont bien des carrés. Note : tous les losanges ont une surface identique, quel que soit le repère.

Ces coordonnées ont le premier avantage de donner une image parlante de ce qu'on nomme l'effet de marée radial : tous les voyageurs vont s’écarter les uns des autres, dans leur espace, leur donnant une "vitesse d'écartement" qui n'est pas pour autant une vitesse relative, une simple déviation de géodésiques inertielles. Je ne m'étend pas là dessus car ce n'est pas le sujet.

La particularité intéressante est que si on prend le même évènement que tout à l'heure, à t=0, Rouge est bien un carré et Vert est un losange au sens d'une vitesse relative locale comme elle serait représentée chez Minkowski. L'angle réciproque de Vert par rapport à Rouge est la vitesse d'un immobile par rapport au voyageur et sa coordonnée temporelle est 0,1*Y. On comprend alors naturellement pourquoi le Y associé à la vitesse de chute vaut exactement le (z+1) local. Y=z+1 est une propriété remarquable des voyageurs issus de l'infini.

On comprend donc que si l'angle de déplacement est donné par la vitesse, la base définit l'espace de cet immobile. Ainsi la courbe violette trouve toute sa justification en tant "qu'espace des immobiles" et on comprend mieux pourquoi elle a cette forme en coordonnées de Painlevé (équivalent des courbes notées 0, Rs/c etc... dans le lien déjà cité, cad une horizontale chez Schwarzschild).

On compend aussi pourquoi l'horizontale en Painlevé comme en Slide est l'espace des voyageurs : c'est la base d'un carré qui représente l'espace-temps local du voyageur Rouge (et des autres). Le Slide est donc continuellement un Minkowski local. Si vous vous posez la question de savoir si le cône passé est symétrique la réponse est non, pouillème de différence mais non.

Pourquoi tout ce bla bla ?

J'ai crée le Slide à l'origine pour tenter de décrire ce que voient les voyageurs en chute libre radialement. L'idée était d'avoir un espace et un temps orthogonaux et de faire "comme chez Minkowski" une projection du cône passé sur une horizontale pour obtenir une distance "vue" (comprendre "distance angulaire" si on plaçait une petite bille à la place du "point" en négligeant la courbure des rayons lumineux non radiaux).

Mais ça ne marche pas... à nouveau pouillème par rapport à ce qui est attendu mais pouillème de trop pour que ça me convienne. Ce qui est attendu c'est simplement que, si on arrive à définir ce que voit un immobile alors ce que voit le voyageur peut être obtenu simplement par application de l'aberration de la lumière en fonction de la vitesse relative par rapport à l'immobile, cad la vitesse de chute. On remarque que le cône passé ne croisera jamais la courbe de l'horizon Rs et donc qu'au fur et à mesure que le voyageur s'approche du trou noir, ce dernier va s'éloigner visuellement (radialement bien sur, inutile de me parler du reste merci).

Si on essaye de faire le même exercice avec Lemaitre on est complètement dans les choux par rapport aux attendus. Pourtant ce système présente, a priori, des caractéristiques "similaires"...

Questions

1/ Etes vous d'accord avec le principe d'application de l'aberration RR entre ce qui est vu par un immobile de Schwarzchild et un voyageur en chute libre ? Justifier un poil la réponse.

2/ Pourquoi est-ce que le Slide ne permet pas de réaliser une projection du cône passé sur un plan euclidien perpendiculaire à la ligne d'univers de Rouge, cad les axes de la figure ?

3/ La plus importante : proposer un système de coordonnées dans lequel on puisse projeter le cône passé pour obtenir ce qui est vu par le voyageur !

Merci d'avance pour votre aide

Mailou
-----

[Mailou75]

Remoi,

Amanuensis, Mach3, Archi3, Jacknicklaus, Yves, Phys4... ou tout autre amoureux de la physique théorique des trous noirs, cette question vous était adressée. Si vous avez peur de la 3, oubliez là, moi même j'avoue qu'elle me fait un peu peur et les formules ne seraient pas sans doute pas élégantes... je voulais surtout m'en servir pour valider ce qui serait obtenu par d'autres moyens.

En fait la 2 aussi n'est pas indispensable, je constate que le Slide ne fonctionne pas pour projeter le cône passé sur un plan euclidien et obtenir une image. J'aurais simplement aimé comprendre pourquoi, et pourquoi Lemaitre ne fonctionne pas non plus... J'aurais aimé comprendre quelles sont les caractéristiques d'un système le permettant sachant que, par exemple, Schwarzschild fonctionne pour l'observateur éloigné.

Donc la vraie question c'est la 1, pour rappel : Etes vous d'accord avec le principe d'application de l'aberration RR entre ce qui est vu par un immobile de Schwarzchild et un voyageur en chute libre ?

Merci d'avance pour votre aide

Mailou

[ordage]

Bonjour Mailou 75

Ces diagrammes illustrent comment le choix des coordonnées illustre plus ou moins bien la (même) solution!

Il faut rappeler que les coordonnées de Painlevé, publiées dans un C.R.A.S d'octobre 1921, suivi d'un autres C.R.A.S en novembre 1921, où il décrit la méthode très élégante, (Painlevé, en plus d'être un homme politique de premier plan, était un excellent mathématicien), qu'il a utilisée, qui en fait définit toute une classe de solutions, puis Mai 1922, où suite à son débat avec Einstein à Paris, il fait une synthèse), a été la première solution non singulière sur l'horizon.

Cela aurait dû ravir Einstein, fort contrarié par ce problème de l'horizon qu'il estimait être une menace pour sa théorie, mais personne n'a compris à l'époque, et sa proposition a été considérée non valide au motifs d'arguments pour le moins fumeux et injustifiés.

Cela a fait que les choses en sont restées là et cette solution est restée méconnue. Quel dommage pour le prestige de la science française. Elle a été remise en valeur (par les anglo-saxons) vers la fin du 20 ième siècle.

Le plus amusant est que Painlevé ne croyait pas à la relativité, mais par contre il en avait compris le formalisme!

Quelques infos complémentaires en :
https://journals.openedition.org/bibnum/851

Cordialement

[Mailou75]

Salut Ordage,

Merci pour ton intervention, j'me sens moins seul

Ces diagrammes illustrent comment le choix des coordonnées illustre plus ou moins bien la (même) solution!

Oui, chaque système va présenter des avantages et inconvénients de "lecture". L'avantage du Slide c'est qu'il permet de rester continuellement en Minkowski local, l'inertiel croisant un espace de plus en plus rapide au cours de sa "chute".

Je me souviens de ton intervention sur un long post traitant des systèmes de coordonnées, et tu m'avais envoyé voir Painlevé, justement.
Un coup de pouce pour lequel je te suis reconnaissant.

Il faut rappeler que les coordonnées de Painlevé, publiées dans un C.R.A.S d'octobre 1921, suivi d'un autres C.R.A.S en novembre 1921, où il décrit la méthode très élégante, (Painlevé, en plus d'être un homme politique de premier plan, était un excellent mathématicien), qu'il a utilisée, qui en fait définit toute une classe de solutions, puis Mai 1922, où suite à son débat avec Einstein à Paris, il fait une synthèse), a été la première solution non singulière sur l'horizon.

Certes mais au prix que l'espace ne soit pas défini en r=Rs. On voit clairement sur le graphe de gauche (Painlevé) que l'espace de l'observateur éloigné de Schw (courbes violettes à t cst) est asymptotique en Rs. La solution est évidement mathématiquement la même et elle ne dit rien de neuf, la position du passage en Rs sera toujours r=Rs t=infini, le point de passage est sur une courbe violette (t) décalée à l'infini vers le haut. Je ne sais pas ce que tu entends par "non singulière", une trajectoire passant Rs visiblement continue ?

.....

Mais ceci n'apporte pas tellement d'eau à mon moulin, la question initiale reste.

Etes vous d'accord avec le principe d'application de l'aberration RR entre ce qui est vu par un immobile de Schwarzchild et un voyageur en chute libre ?

A+

Mailou

[A voir en vidéo sur Futura]

[ordage]

Bonjour
Pour essayer de répondre à tes questions:
1- Si je comprends bien ta question, je pense que la réponse est "oui": Dans un CRAS du 10/04/1922, Sauger déduit la métrique de Schwarzschild en 3 lignes de calcul à partir de la métrique de Minkowski en considérant le point de vue d"un observateur à l'infini sur la mesure dR et dT d'un référentiel attaché à un observateur en chute libre radiale, situé à une coordonnée spatiale r, animé une vitesse v = -sqrt(2GM/r), qu'il ferait d'un élément local pour lui (à l'infini sans boost) dr et dt, en appliquant les formules de Lorentz.
2- Ta transformation conduit-elle à un diagramme qui peut être décrit par une métrique globale se déduisant des autres par un changement de coordonnées? Au niveau local , il existe un espace temps de Minkowski, mais c'est trivial. A noter que les sections spatiales (à T = cste) sont euclidiennes dans la métrique de Painlevé.
3- Je ne comprends pas le problème. Le "cône" de lumière local , si on le prolonge à l'infini par les géodésiques nulles qui le délimitent,(ce qui donne un cône" déformé) définissent tout le passé qui pu influer sur le présent et tous les objets concernés et ce qu'il peut voir.

Remarques: la notion d'éléments statiques, qui ne sont pas inertiels, ce qui suppose un espace statique, est assez conventionnelle. Aujourd'hui, on considère plutôt que l'espace n'est pas statique, mais stationnaire en effondrement continu (v = -sqrt(2GM/r)), et qu'en fait ce sont les observateurs de Painlevé qui sont statiques (co-mobiles de l'effondrement de l'espace) et ceux de Schwarzschild sont en mouvement (accélérés). Cette approche a été bien explicité par Lemaître (d'où sa forme) qui considérait la solution de Schwarzschild comme un cas particulier d'univers cosmologique ' voir chapitre 11 de son article "L'univers en expansion" 1932.

J'espère avoir répondu au moins partiellement à tes questions
Cordialement

[Mailou75]

Salut Ordage,

Désolé pour l’absence de réponse mais j'ai décroché ces derniers temps. Pas dis que j'y retourne d'aillleurs, à part pour aller au fond de l'impasse...

1- Si je comprends bien ta question, je pense que la réponse est "oui": Dans un CRAS du 10/04/1922, Sauger déduit la métrique de Schwarzschild en 3 lignes de calcul à partir de la métrique de Minkowski en considérant le point de vue d"un observateur à l'infini sur la mesure dR et dT d'un référentiel attaché à un observateur en chute libre radiale, situé à une coordonnée spatiale r, animé une vitesse v = -sqrt(2GM/r), qu'il ferait d'un élément local pour lui (à l'infini sans boost) dr et dt, en appliquant les formules de Lorentz.

Effectivement, en prenant simplement Newton et en imposant la RR locale (Minkowski) on obtiendrait le Slide : la trajectoire des immobiles est le symétrique d'une chute libre chez Newton (r;T) Tau temps propre avec la formule que tu rappelles ; localement on a des petits diagrammes de Minkowski, car croisement avec l'espace avec une vitesse relative connue. On en déduit la forme de "l'espace des immobiles" qui par changement de coordonnées donne la métrique de Schw. Ça ne doit marcher que pour une dimension, sinon il n'y aurait pas de différence entre Newton et Einstein

Moi je veux bien que ce soit le cas, qu'on applique l'aberration RR, même ça m’arrangerait puisque ça me semble logique. Le problème c'est les conséquences : lorsqu'on chute vers un trou noir sa surface (ou du moins un évènement à Rs+epsilon) sera vue à l'infini, du fait de l'aberration... voir Blueshift et apparence d'un objet "en approche" quand la vitesse relative tend vers c. C'est à l'opposé de ce qu'on entend, même si ici on ne traite que la radiale, faut bien que je commence par le plus simple.

Une question liée qui pourrait aider : Mettons que je sois le dernier à sauter (graph qu message 1), au moment où je passe l'horizon je verrai tous ceux qui ont sauté avant moi, au moment où eux même passent l'horizon, parce que l'horizon est un rayon lumineux. A quelle distance* les verrais-je ? Je fournis avec plaisir sur demande la seule donnée utile : intervalle de temps d'arrivée à la singularité en unité adimensionnée Rs/c.

*quand on parle de "voir" il s'agit de la distance angulaire. Dans le cas présent on suppose une petite bille, en négligeant la courbure des rayons non radiaux. "Voir" comme tout résultat d'un calcul portant sur l'aberration lumineuse. "Voir" comme distance angulaire en cosmo. Etc

2- Ta transformation conduit-elle à un diagramme qui peut être décrit par une métrique globale se déduisant des autres par un changement de coordonnées? Au niveau local , il existe un espace temps de Minkowski, mais c'est trivial.

Oui c'est juste un changement de coordonnées. Une translation sans changement d'échelle selon r. Il suffit de retrancher la coordonnée r du chuteur concerné (le Slide ne vaut que pour un observateur) aux coordonnées de Painlevé. C'est juste une soustraction sur la coordonnée r, mathématiquement. Peut-être que la "métrique" globale sera inélégante mais elle doit exister, je suppose.

A noter que les sections spatiales (à T = cste) sont euclidiennes dans la métrique de Painlevé.

Oui ça je sais. Étrangement celui qui chute depuis l'infini et celui qui y reste (Schw) partagent le même "espace". On voit que les abscisses de Schw et de Painlevé sont les mêmes : r ! C'est lié au fait que le Y (gamma) lié à la vitesse locale de chute vaut exactement le z+1 (Redshift gravitationnel) pour un r donné. Traduction : quand celui qui est à l'infini voit un intervalle entre deux valeurs de r infinitésimales compressé (de z+1) par rapport à l'intervalle de longueur propre (l'obs de Schw "voit" vraiment l'intervalle r) alors, celui qui est en train de chuter voit/mesure latéralement (Doppler transverse) un espace compressé de Y. Comme les deux ont la même valeur, nos deux observateurs ont chacun le droit d'utiliser r mais pas pour les mêmes raisons. Schw s'en sert pour projeter son cône passé (façon Minkowski avec un cône conique) l'autre apparemment pas sinon je ne poserais pas ma question

3- Je ne comprends pas le problème. Le "cône" de lumière local , si on le prolonge à l'infini par les géodésiques nulles qui le délimitent,(ce qui donne un cône" déformé) définissent tout le passé qui pu influer sur le présent et tous les objets concernés et ce qu'il peut voir.

Oui bien sur. N'importe quel système nous donnera les mêmes informations : quels évènements seront vus simultanément par un observateur. Mais aucun ne dis "comment" ils seront "vus" (voir définition plus haut) à part Schw pour l'observateur éloigné, d'après ce que j'ai compris. Ce que je cherche justement c'est un repère où je puisse projeter un cône passé sur un plan euclidien (façon Minko/Schw) pour un observateur en chute libre. A nouveau je commence par le plus simple, celui qui tombe depuis l'infini. Le résultat pourrait être très ressemblant au Slide car lui même donne quasiment le résultat attendu, cad l'aberration RR par rapport à ce que voit un immobile. Donc sous réserve que 1 ce soit juste, 2 j'ai correctement interprété ce que voit un immobile en r (ça pourrait aussi être un sujet...). Tu la vois la l'impasse ?

Remarques: la notion d'éléments statiques, qui ne sont pas inertiels, ce qui suppose un espace statique, est assez conventionnelle. Aujourd'hui, on considère plutôt que l'espace n'est pas statique, mais stationnaire en effondrement continu (v = -sqrt(2GM/r)), et qu'en fait ce sont les observateurs de Painlevé qui sont statiques (co-mobiles de l'effondrement de l'espace) et ceux de Schwarzschild sont en mouvement (accélérés). Cette approche a été bien explicité par Lemaître (d'où sa forme) qui considérait la solution de Schwarzschild comme un cas particulier d'univers cosmologique ' voir chapitre 11 de son article "L'univers en expansion" 1932.

Lemaître avait compris pas mal de trucs je crois, je ne suis pas encore à jour... Son système de coordonnées à le même avantage que le Slide avec une ordonnée en Tau régulier, mais valable cette fois pour tous les chuteurs consécutifs + l'horizon est à 45° + les immobiles sont rectilignes, parallèles avec un temps propre régulier. Répondre à toutes ces contraintes c'est une prouesse ! Toutefois, je l'ai essayé pour le présent sujet, sans succès. C'est toute la question : Slide et Lemaitre ont tous deux une ligne d'univers verticale à ponctuation régulière, a priori un "espace euclidien de projection" perpendiculaire donc horizontal, pourtant : 1 ils ne donnent pas le même résultat 2 ils sont tous les deux "faux" pour ce sujet. D'où la question : quelles sont les caractéristiques d'un système qui répondrait à la seule contrainte que je fixe ici : pouvoir projeter le cône passé sur un plan ! A nouveau sous réserve que l'interprétation d'équivalent aberration soit juste. Et dans le domaine peu de références puisque tout dit le contraire. Re impasse... bref

Merci pour ton aide, a +

Mailou

[mach3]

Une idée qui me vient comme ça, suite aux autres discussions sur Painlevé. Au lieu de faire une translation le long de r pour que la ligne d'univers du chuteur soit représentée par une verticale, ne serait-ce pas mieux de dilater r (façon facteur d'échelle) en fonction de t_r pour obtenir la même représentation verticale de cette ligne d'univers ?

m@ch3

[Mailou75]

Une idée qui me vient comme ça, suite aux autres discussions sur Painlevé. Au lieu de faire une translation le long de r pour que la ligne d'univers du chuteur soit représentée par une verticale, ne serait-ce pas mieux de dilater r (façon facteur d'échelle) en fonction de t_r pour obtenir la même représentation verticale de cette ligne d'univers ?

Pas bien compris. Peux tu préciser ?

As tu compris le sens des petits Minkowski dans le Slide ? Ne sont-ils pas extrêmement instructifs ?

Pourrais-je avoir ton opinion sur le sujet du fil stp ?

Etes vous d'accord avec le principe d'application de l'aberration RR entre ce qui est vu par un immobile de Schwarzchild et un voyageur en chute libre ?

[mach3]

On pose une nouvelle variable radiale, r, fonction de A le rayon aréal, telle qu'elle vaut constamment 1 pour un chuteur qui atteint le rayon aréal nul pour t_r=0 :

(sauf erreur)

Ainsi la ligne d'univers de ce chuteur libre est redressée (mais seulement celle-là, si on ne compte pas le fait que chaque point est une sphère et donc chaque chute radiale et une coquille en chute radiale), c'est une verticale d'abscisse r=1, et l'espace reste euclidien et est représenté perpendiculairement à cette ligne. La seule particularité, c'est que l'échelle horizontale dépendra de la valeur de t_r (comme en cartographie où l'échelle horizontale peut dépendre de la latitude). Pour le coup on peut vraiment générer chaque tranche spatiale de manière fidèle par rotations suivant theta et phi, c'est juste que les distances réelles entre deux points de même r,theta,phi vont diminuer avec t_r (et à l'inverse, deux points situés à une distance réelle constante vont être représentés de plus en plus éloignés avec t_r).

Pour le sujet principal du fil, pour l'instant je ne me prononce pas, ça fait longtemps qu'il me fait de l'oeil mais que je ne parviens pas à entrer dedans. La tentative de redresser un chuteur libre est intéressante et la solution considérée pour le faire (la translation), n'est peut être pas la meilleure, d'où ma proposition de dilater plutôt que de translater.

m@ch3

[ordage]

On pose une nouvelle variable radiale, r, fonction de A le rayon aréal, telle qu'elle vaut constamment 1 pour un chuteur qui atteint le rayon aréal nul pour t_r=0 :

(sauf erreur)

Ainsi la ligne d'univers de ce chuteur libre est redressée (mais seulement celle-là, si on ne compte pas le fait que chaque point est une sphère et donc chaque chute radiale et une

bonjour
Quelle serait la métrique avec cette coordonnée r.

Comme


est l'équation géodésique , il me semble que tu obtiens quelque chose qui ressemble à la métrique de Lemaître (où les géodésiques sont des verticales) et où la variable t est remplacée par( t-T), où t est l' étiquette d'un observateur qui permet de les identifier (identifie les différentes verticales).
Cordialement

[ordage]

Correction T à la place de t

bonjour
Quelle serait la métrique avec cette coordonnée r.

Comme


est l'équation géodésique , il me semble que tu obtiens quelque chose qui ressemble à la métrique de Lemaître (où les géodésiques sont des verticales) et où la variable t est remplacée par( t-T), où T est l' étiquette d'un observateur qui permet de les identifier (identifie les différentes verticales).
Cordialement

[mach3]

Attention, pas de confusion, le rayon aréal est noté A (ce qu'on note r bien souvent dans les ouvrages). Le r que je propose n'est pas rayon aréal. Désolé je n'ai pas été assez précis. Je développerai mieux dans un prochain post

m@ch3

[Mailou75]

Salut,

Je veux bien essayer et essayer de trouver le temps

J’aimerai comprendre un peu ce que tu cherches à obtenir :
- ton t_r c’est le temps propre tau de Painlevé ?
- quelles sont les trajectoires verticales ? La singularité, l’horizon, un seul chuteur mais lequel ?

J’ai l’impression que ta formule a des similitudes avec Lemaitre, faut que je regarde...

A+

[yves95210]

J’ai l’impression que ta formule a des similitudes avec Lemaitre, faut que je regarde...

Avec la dernière équation figurant dans ce message, certainement... Il s'agit d'une des solutions de la métrique de Lemaître-Tolman, dont Schwarzschild et Friedmann-Lemaître sont des cas particuliers (respectivement en espace vide et en espace de densité de matière homogène), exprimée dans un système de coordonnées où est le temps propre des particules "comobiles" (alias en chute libre) et les hypersurfaces spatiales sont orthogonales à l'axe des .
Donc ce n'est étonnant de retrouver ici la même expression du rayon aréal que dans la métrique de LT "Schwarzschild like", dans le vide autour d'une masse centrale. D'ailleurs, en disséquant ce cas particulier, on était tombé sur les coordonnées de Painlevé.

Les solutions de la métrique de LT s'expriment en fonction de trois fonctions arbitraires de la coordonnée radiale, , et (je note ici la coord radiale R pour éviter la confusion avec le r de mach3). est la masse de la boule de rayon R (de manière générale l'espace décrit par cette métrique présente une symétrie sphérique, mais n'est pas vide) et peut être vu comme l'énergie totale (cinétique + potentielle) d'une particule de masse unitaire de coordonnée radiale R, puisqu'on a . En particulier, quand on obtient simplement

Au passage, le cas E=0 pour tout R, dont il est question dans le premier message en lien et ailleurs dans la discussion sur la métrique de Lemaître-Tolman, est le seul qui correspond à une courbure spatiale (partout) nulle si la densité de matière est homogène (ce qui est évidemment le cas de l'espace vide). Je pense l'avoir prouvé en réponse à un MP de mach3 qui avait un doute sur ce point, mais il ne m'a pas confirmé s'il était d'accord avec la démonstration... Si tu veux je peux de transférer ce MP.

[mach3]

Salut,

Je vais expliquer plus proprement pour dissiper de possibles mal entendus. On part de l'expression de Painlevé de la métrique de Schwarzschild :


est le temps propre des chuteurs venant de l'infini avec une vitesse nulle, A est le rayon aréal et est la métrique de la sphère

Les tranches spatiales de t_r constant sont euclidienne et les géodésiques des chuteurs, orthogonales à ces tranches spatiales, sont contraintes par , ce qui après intégration donne des courbes d'équation (équation déjà citée, pas exactement sous cette forme), avec t_r0 une constante qui identifie le chuteur par sa date d'arrivée à la singularité

Dans le post initial, il est proposé de modifier le système de coordonnées pour que la géodésique d'un des chuteurs soit une verticale. Ainsi l'orthogonalité entre cette géodésique et les tranches spatiales est réalisée dans la représentation.

L'option choisie est de décaler les abscisses vers la droite au fur et à mesure que t_r progresse. La nouvelle variable radiale est . t_r0 étant une constante, la date à laquelle l'unique chuteur selectionné atteint la singularité

Une autre option (ma proposition) est de redimensionner les abscisses plutôt que de les décaler. La nouvelle variable radiale est alors . t_r0 étant une constante, la date à laquelle l'unique chuteur selectionné atteint la singularité

Dans les deux cas, la géodésique du chuteur sélectionné est représentée par une droite verticale et la représentation des tranches spatiales de t_r constant ne semble pas altérée (à confirmer pour la première option, certain pour la seconde).

Une autre option bien connue pour redresser cette géodésique est l'utilisation des coordonnées de Lemaitre, qui font du zèle et redressent les géodésiques de tous les chuteurs, mais avec lesquelles la représentation des tranches spatiales est altérée.

Concernant le rapprochement avec LTB, j'ai quelques doutes car à part pour le Lemaitre où les lignes de coordonnée radiale constante sont des géodésiques par construction, j'ai des doutes pour les deux autres. En LTB, ces lignes de coordonnée radiale constante doivent être des géodésiques.

Je n'ai pas encore bien saisi l'objectif du premier post, ni chercher à adresser les questions qui y sont posées, mais les dernières discussions sur Painlevé m'ont inspiré cette deuxième option, qui peut être présentera un intérêt pour mailou.

m@ch3

[mach3]

Bon, ce qui me bloque c'est ça :

L'idée était d'avoir un espace et un temps orthogonaux et de faire "comme chez Minkowski" une projection du cône passé sur une horizontale pour obtenir une distance "vue" (comprendre "distance angulaire" si on plaçait une petite bille à la place du "point" en négligeant la courbure des rayons lumineux non radiaux).

Je ne trouve aucune justification à cela a priori. Comme je ne comprend pas pour quelle raison cela devrait fonctionner, je suis bien en peine d'expliquer pourquoi ça ne marche pas...

Je reviendrais si j'ai un déclic.

m@ch3

[ordage]

Attention, pas de confusion, le rayon aréal est noté A (ce qu'on note r bien souvent dans les ouvrages). Le r que je propose n'est pas rayon aréal. Désolé je n'ai pas été assez précis. Je développerai mieux dans un prochain post

m@ch3

Bonjour

La coordonnée r de cette équation géodésique est celle de la partie 2D, à symétrie sphérique, de la métrique:
dS² = r² ( d_theta² + sin² (theta) . d_phi²).

Je suppose que c'est ce que tu appelle le rayon aréal?

En fait pour avoir des géodésiques représentées par une verticale dans un diagramme orthogonal T, t (où T est une cordonnée d'espace et t une coordonnée de temps), il faut que T soit constant pour la géodésique, donc qu'il soit une coordonnée co-mobile. (comme en cosmologie)

C'est la métrique de Lemaître, son approche de type cosmologique (il a traité ce problème dans son article l'univers en expansion -1932) étant que pour le problème autour du corps central (dans le vide) à symétrie sphérique, le vide est dynamique (en effondrement) et que les observateurs en chute libre radiale ne sont pas en mouvement mais "immobiles" (en fait co-mobiles) dans l'espace, ce qui est l'approche moderne.
Notons qu'on obtient toute les géodésiques pour toutes les valeurs de T qui est une étiquette, associée à une géodésique, qui peut être définie par exemple par la "date" de leur arrivée de l'observateur associé, à r = 0+.
J'ai appelé cette variable T , mais elle est appelée R dans le Landau-Lifchitz et "Psi" chez Lemaître.
Cordialement

[Avatar10]

Une lecture intéressante: http://www.bibnum.education.fr/sites...leve_these.pdf

[yves95210]

Une lecture intéressante: http://www.bibnum.education.fr/sites...leve_these.pdf

J'ai déjà vu ça quelque-part Mais oui, c'est très intéressant.

[Avatar10]

Je n'avais pas lu ce fil...bon ben, pas grave, dès fois une redite n'est pas superflue (au moins pour le lecteur silencieux).

[yves95210]

Concernant le rapprochement avec LTB, j'ai quelques doutes car à part pour le Lemaitre où les lignes de coordonnée radiale constante sont des géodésiques par construction, j'ai des doutes pour les deux autres. En LTB, ces lignes de coordonnée radiale constante doivent être des géodésiques.

Le lien avec LTB : je pars de


et


On peut étiqueter une famille d'observateurs en chute libre radiale depuis l'infini par l'instant auquel ils atteignent la singularité, définir une nouvelle coordonnée radiale telle que en soit une fonction strictement croissante et faire le changement de coordonnées . En notant la dérivée d'une fonction par rapport à et sa dérivée par rapport à ,


Alors


En injectant cette expression dans celle de la métrique, on retombe sur l'expression habituelle de la métrique LTB dans le cas pour tout ,

[Mailou75]

Salut,

Merci pour vos réponses,

Les solutions de la métrique de LT s'expriment en fonction de trois fonctions arbitraires de la coordonnée radiale, , et

M, E, T ça me rappelle quelque chose
J'aime bien l'idée de creuser LTB c'était bien parti, j'attends toujours votre exemple d'épaisseur/densité de coques concentriques, le fil a été perdu...
J'avoue que j'ai essayé de suivre de loin mais c'est trop matheux pour moi.
En tout cas dans le principe je suis pour. Faut essayer de faire un truc synthétique et si possible avec des dessins pour ceux qui ne lisent pas le mandarin
Par contre si on pouvait faire ça ailleurs que sur ce fil ça évitera le bordel, mci.

.....

ce qui après intégration donne des courbes d'équation

D'accord, Ordage, Yves et toi êtes donc d'accord, aux notations près...

La nouvelle variable radiale est .

Pas si moche, merci pour la formule

La nouvelle variable radiale est alors

Ok tant qu'Excel me sort ton r_mach3 en fonction de t_r, no problemo.

Par contre il faut que tu me décrives à quoi va ressembler le résultat. Une trajectoire de chute sera verticale, mais encore ?.. La singularité, l'horizon, les autres chuteurs, à quoi je dois m'attendre ? A l'aveugle c'est un peu tendu... je suis pas une Texas Instrument, je bosse "à la main"

Je ne trouve aucune justification à cela a priori. Comme je ne comprend pas pour quelle raison cela devrait fonctionner, je suis bien en peine d'expliquer pourquoi ça ne marche pas...

J'imagine que tu es d'accord que ça fonctionne pour Minkowski, l'aberration. Ici https://forums.futura-sciences.com/p...ml#post6423022 on peut voir que le contenu du cône passé est projeté verticalement sur l'espace euclidien pour former de qui est vu : le ~losange rouge

J'ai cru comprendre qu'on pouvait faire pareil pour Schw, pour les immobiles, compris celui à l'infini. Ici https://forums.futura-sciences.com/d...ml#post6441871 le repère de droite est celui de l'observateur à l'infini (gris), il "est un cube local 2D+t" et voit les autres immobiles (en vert) compressés radialement et reshiftés étirés dans le temps ; à coté c'est le repère du stationnaire à 2,97Rs, il "est un cube local 2D+t" et voit les autres immobiles compressés ou étirés radialement suivant s'il se trouvent au dessous ou en dessus de lui. Tous les parallélépipèdes on le même volume, comme les immobiles ne changement pas de place (pléonasme) le contenu du cône et celui du plan euclidien sont identiques, à la date de l'évènement observé près...
J'ai cru comprendre que t'avais encore des doutes là dessus

A l'autre bout de la lorgnette, on a une réponse "commune" (mais relativement peu étayée) qui consiste à dire que si on connaît ce que voit un immobile en r, alors pour savoir ce que voit un chuteur passant en r il suffit d'appliquer l'aberration RR, avec la vitesse locale de chute (1). Je suis d'accord pour dire que c'est indispensable localement, mais je n'en ai aucune certitude à distance... aucune raison pour que ce soit le cas. Les évènements vus resteront toujours les mêmes mais les déformations n'ont aucune raison d'être "comme chez Minko" bien au contraire !

Donc, puisque l'objectif est de connaître ce que voit le chuteur je peux toujours faire cette conversion (d'ailleurs je l'ai faite) mais je la compare à quoi ? Je la valide comment ? Alors je cherche un repère "de projection", je tombe sur le Slide. Ça ne marche pas. Ou du moins ça ne marche pas si (1) est vrai... what else George ? Bien sur on ne trouve aucun document "intermédiaire" entre un Kruskal flou et la vidéo de Riazzuello, ça fait un gap pour suivre le fil ! Moi j'aimerais déjà savoir comment on voit une bille ou un cube, on verra après pour le cosmos

Merci, a +

Mailou

[yves95210]

Salut Mailou,

Un chuteur atteint l'horizon (s'il ne se fracasse pas sur la surface d'un corps central de rayon supérieur à son rayon de Schwarzschild ) quand .
Alors, en notant l'instant où le chuteur de coordonnée radiale constante atteint l'horizon,



Comme le changement de variable proposé consiste à utiliser une fonction strictement croissante de comme coordonnée radiale, sur ton graphique tu peux aussi bien considérer que l'axe horizontal représente les valeurs de (ça revient à choisir la fonction la plus simple, ).
Si l'échelle de temps utilisée sur les deux axes est la même, avec une origine en , , la singularité centrale sera représentée par une demi-droite à 45° partant de l'origine, et l'horizon par une autre demi-droite à 45°, partant du point , .

Je suppose que tu as besoin de l'équation de la trajectoire des "immobiles", les objets pour lequel est constant.
Pour qu'un immobile situé sur la sphère de rayon aréal croise un comobile de coordonnée radiale à l'instant , il faut que


Tes immobiles sont donc aussi représentés par des droites à 45°, passant par le point

[ordage]

Bonjour
Il me semble que la forme que tu proposes c'est celle de Lemaître dont le diagramme est donné ci-dessous, cf Landau-Lifchitz.



En fait, les formes de Painlevé et de Lemaître sont sont apparentées car elles dérivent d'une même forme générique.(cf Lemaître)
Cordialement

[yves95210]

Il me semble que la forme que tu proposes c'est celle de Lemaître dont le diagramme est donné ci-dessous, cf Landau-Lifchitz.

Pièce jointe 449652

En fait, les formes de Painlevé et de Lemaître sont sont apparentées car elles dérivent d'une même forme générique.(cf Lemaître)
Cordialement

Oui, bien sûr. Mais la métrique de Lemaître-Tolman dont, entre autres, Schwarzschild (quel que soit le système de coordonnées utilisé, Schw., Painlevé, Lemaître, etc.) est un cas particulier, est encore plus générale puisque la seule hypothèse est l'isotropie de l'espace (symétrie sphérique), sans contrainte d'homogénéité (comme FLRW, autre cas particulier) ou d'espace vide (comme Schw.).
Et il se trouve que, pour répondre à la question posée par Mailou, l'utilisation de la métrique de LT avec E=0 (=> espace plat) et du système de coordonnés dans lequel on l'exprime habituellement (il me semble qu'il a été formalisé par Bondi, une quinzaine d'années après les papiers de Lemaître et de Tolman) donne le résultat directement. Donc, pourquoi s'en priver...?

Au passage, je trouve dommage que cette solution ne soit pas enseignée dès les cours d'introduction à la RG (en tout cas je ne l'ai pas rencontrée dans ceux que j'ai parcourus), car sa dérivation n'est guère plus compliquée que celles de la métrique de Schw. ou de la métrique FLRW et le passage de LT à l'un ou l'autre de ces cas particuliers est assez simple, alors qu'elle permet de traiter, assez simplement aussi, d'autres problèmes d'intérêt (comme par exemple l'effondrement (ou l'expansion) d'une zone de sur (ou sous-)densité, la formation de l'horizon d'un trou noir, etc.).
Certes il y a des raisons historiques pour cela : les premières solutions analytiques trouvées à l'équation d'Einstein ont été celles de Schw. et Friedmann-Lemaître, et les prédictions qu'elles ont permis de faire ont été les premières à être vérifiées expérimentalement. Mais l'ordre chronologique n'est pas toujours le plus pédagogique...

[mach3]

@Yves, j'ai l'impression qu'il y a méprise. Ce que tu proposes, c'est de la même famille que l'option Lemaitre, qui rend verticales toutes les géodésiques de chute libre depuis l'infini à vitesse nulle.
La fonction par laquelle je divise le rayon aréal est avec un tr0 constant, indépendant du chuteur et ne redresse du coup que la géodésique du chuteur qui atteint la singularité en tr0, pas les autres.

J'ai ajouté une précision dans ce sens dans mon message précédent

Par contre il faut que tu me décrives à quoi va ressembler le résultat. Une trajectoire de chute sera verticale, mais encore ?.. La singularité, l'horizon, les autres chuteurs, à quoi je dois m'attendre ? A l'aveugle c'est un peu tendu... je suis pas une Texas Instrument, je bosse "à la main"

La ligne d'univers du chuteur sélectionné (pas celle des autres), devient verticale, comme dans le slide. La singularité reste par contre en r=0, comme chez Painlevé. Les tranches spatiales sont euclidiennes et leur représentations se dilatent au fur et mesure que tr approche de tr0, de façon à ce que la ligne d'univers du chuteur reste droite. Evidemment, il y a singularité de coordonnée pour tr=tr0, car la dilatation devient infinie. On ne peut pas décrire ce qui se passe après (en terme de tr) l'arrivée du chuteur à la singularité. Vraisemblablement, l'horizon sera une courbe ayant r=0 et tr=tr0 comme asymptotes.

J'imagine que tu es d'accord que ça fonctionne pour Minkowski, l'aberration. Ici https://forums.futura-sciences.com/p...ml#post6423022 on peut voir que le contenu du cône passé est projeté verticalement sur l'espace euclidien pour former de qui est vu : le ~losange rouge

Ca semble marcher (ça demanderait un examen plus approfondi), mais si ça marche c'est parce que l'espace-temps est plat. Si ça marche, ça ne peut pas marcher en espace-temps courbe.

Pour décrire ce qui est vu dans le cas général, il faut utiliser les géodésiques nulles. Leurs projections sur des tranches spatiales plates est univoque en espace-temps plat, donc ça doit permettre des raccourcis, mais ça n'est plus possible quand l'espace-temps est courbé.

Là où c'est correct, c'est qu'à partir du moment où on a pu calculer ce que voit un observateur donné en un évènement donné, il est possible de calculer ce que voit un autre observateur, en mouvement par rapport au premier en ce même évènement, grâce au doppler et à l'aberration. Toute la difficulté est de calculer une première fois pour un observateur. Il existe peut-être un système de coordonnée qui facilite cela pour un observateur particulier, mais de toutes façon il faut se farcir les geodesiques nulles, et hors du cas radial, ce n'est pas de la tarte...

m@ch3

[yves95210]

@Yves, j'ai l'impression qu'il y a méprise. Ce que tu proposes, c'est de la même famille que l'option Lemaitre, qui rend verticales toutes les géodésiques de chute libre depuis l'infini à vitesse nulle.
La fonction par laquelle je divise le rayon aréal est avec un tr0 constant, indépendant du chuteur et ne redresse du coup que la géodésique du chuteur qui atteint la singularité en tr0, pas les autres.

Je n'ai pas forcément bien compris ce que Mailou recherchait... Mais la solution que je proposais (qui n'est finalement qu'une généralisation de la tienne, moyennant l'utilisation de \tau_0 pour étiqueter les chuteurs), a l'avantage de redresser les géodésiques de tous les chuteurs, de répondre simplement à la question qu'il posait dans son dernier message,

Par contre il faut que tu me décrives à quoi va ressembler le résultat. Une trajectoire de chute sera verticale, mais encore ?.. La singularité, l'horizon, les autres chuteurs, à quoi je dois m'attendre ?

et à celle qu'il n'avait pas posée dans ce message (la trajectoire des "immobiles").

Si ce n'était pas le but (ou une étape utile vers ce but), je vous prie de m'excuser pour le hors-sujet.

[Mailou75]

Salut et merci pour vos réponses,

Là je reconnais la chute libre de Newton.

..........

Il me semble que la forme que tu proposes c'est celle de Lemaître

Oui, comme la description semblait coller (tout le monde à 45°) je suis allé verifier. C'est exactement la même chose.

..........

(...) donne le résultat directement. Donc, pourquoi s'en priver...?

Effectivement, en nombre de lignes de calcul ça a l'air plutôt léger

..........

La ligne d'univers du chuteur sélectionné (pas celle des autres), devient verticale, comme dans le slide. La singularité reste par contre en r=0, comme chez Painlevé. Les tranches spatiales sont euclidiennes et leur représentations se dilatent au fur et mesure que tr approche de tr0, de façon à ce que la ligne d'univers du chuteur reste droite. Évidemment, il y a singularité de coordonnée pour tr=tr0, car la dilatation devient infinie. On ne peut pas décrire ce qui se passe après (en terme de tr) l'arrivée du chuteur à la singularité. Vraisemblablement, l'horizon sera une courbe ayant r=0 et tr=tr0 comme asymptotes.

Ok, ça se précise un peu, r=0 et LE chuteur choisi sont verticaux, c'est l'horizon qui se déplace. Le mieux, si t'as encore mon mail c'est que m'envoies un p'tit dessin de ce que tu imagines, ça ira tellement plus vite. Et ça m'aiderait beaucoup. Est-ce que tu penses que le système aura un intérêt ? Je ne voudrais pas non plus bosser pour rien... Merci

Pour décrire ce qui est vu dans le cas général, il faut utiliser les géodésiques nulles. Leurs projections sur des tranches spatiales plates est univoque en espace-temps plat, donc ça doit permettre des raccourcis, mais ça n'est plus possible quand l'espace-temps est courbé.

Non stp, c'est hors sujet. Quand on fait de la RR en 1D+t et qu'on dit "est vu à telle distance" on ne se prends jamais la tête, et chaque fois que j'utilise le même terme en RG c'est la levée de bouclier. Si tu considères qu'en 1D on ne peut pas lire les graduations d'un mètre ruban c'est que tu limites ton abstraction. Le mètre lui même n'existe même pas en 1D, ni ses graduations... Je ne discute pas sur ce terrain. La seule définition que je peux te redonner c'est qu'on regarde des billes infinitésimales avec de super instruments de haute précision et qu'on néglige donc la courbure des rayon non radiaux ce qui revient à une distance angulaire. Tu la prends ou pas mais ça ne m'intéresse pas de discuter ce sujet, je l'ai déjà trop fait.

Pour te dire à quel point c'est bête et méchant : imagine qu'en 2D+t tu aies un mirage gravitationnel. Et bien ta carte plane de "ce qui est vu" présentera deux endroits différents pour un seul et même lieu (peut être le même évènement si le mirage est parfaitement symétrique). En 3D ce serait comme un espèce de solide de ce qui est vu. De la même façon on aurait pas des rayon courbes qui contournent une masse mais un cercle d'évènements identiques. Ce-qui-est-vu, on se fout du pourquoi comment.

Ca semble marcher (ça demanderait un examen plus approfondi), mais si ça marche c'est parce que l'espace-temps est plat. Si ça marche, ça ne peut pas marcher en espace-temps courbe.

Oui c'est l'aberration, bien sur que ça marche

Là où c'est correct, c'est qu'à partir du moment où on a pu calculer ce que voit un observateur donné en un évènement donné, il est possible de calculer ce que voit un autre observateur, en mouvement par rapport au premier en ce même évènement, grâce au doppler et à l'aberration.

Tu viens de dire strictement l'inverse à la citation précédente. Dommage c'est exactement la réponse que je souhaitais, sauf que tu me la sors avec une contradiction accolée...
Si l'aberration ne marche pas en espace temps courbe alors on ne peux pas transformer des "visons d'observateurs" en celles d'autres ayant une vitesse relative.
Pourtant je finis par me convaincre que c'est la seule solution possible pour ne pas finir le puzzle au marteau !

Toute la difficulté est de calculer une première fois pour un observateur [immobile]

Ca ne me semblait pas si difficile mais tu émets des doutes sur mon point de vue, du coup je doute aussi, mais c'est pareil, je ne peux pas complètement douter sans envoyer valser tout le puzzle...

..........

Je n'ai pas forcément bien compris ce que Mailou recherchait...

Tout d'abord la citation de mach3 que j'ai mis en orange (de préférence sans contradiction) : peut-on utiliser l'aberration RR entre un immobile et un chuteur chez Scwh ?

Ensuite un repère qui permette de projeter un cone passé 1D sur une ligne pour en faire une distance angulaire. Pour te répondre, Lemaitre ne marche pas, c'est même le premier que j'ai essayé avec sa trajectoire de chute verticale et réputé être "le référentiel des chuteurs depuis l'infini". Il marche même très mal au point que je n'ai eu aucun doute à l'éliminer. Le Slide par contre est très proche de repère recherché, il donne quasiment les bons résultats. Je me demandais donc, qu'est ce qui fait qu'un repère pourrait permettre de projeter le cone passé sur un plan euclidien. Ca marche chez Minko, a priori en coordonnées de Schw, pourquoi pas les autres ?

Merci A+

Mailou

[mach3]

La suite de la conversation dérivant de Painlevé, une nouvelle discussion a été créée :

https://forums.futura-sciences.com/d...ion-rr-rg.html

mach3, pour la modération