définition du vrai en math

[Médiat]

0.99999999999.... avec une suite de 10 puissance 43 fois le nombre 9 est une mesure physique qui n'est pas égale à 1, tant s'en faut.
En Math, on dira que c'est le nombre 1

Dans le domaine du "c'est pas parce que je n'y connais rien que je ne donne pas mon avis péremptoirement", un record vient d'être battu !

-----

[invite51d17075]

0.99999999999.... avec une suite de 10 puissance 43 fois le nombre 9 est une mesure physique qui n'est pas égale à 1, tant s'en faut.
En Math, on dira que c'est le nombre 1

La concrétisation de ce problème ou de manifestation d'une des différences épistémologiques profonde et essentielle entre math et physique se manifeste obviously dans la mesure de la courbure de l'univers.

Merci de corriger si je me trompe

Oui, deux fois.
c'est évidemment faux en math, car si la suite de 9 est interrompue , ce ne sera jamais le nb 1. c'est trivial
en physique, le pb est d'un autre ordre.
on fait face à une incertitude , ce qui n'a rien à voir avec un nb de décimales.
et celle-ci ( liée entre autres à nos diff mesures ) tourne autour de 1 et sans chiffre précis même si l'intervalle couvre d'avantage une valeur potentielle >1 ( mais qui n'exclus pas l'opposé ).

donc la comparaison est au mieux maladroite, et au pire "à coté de la plaque". (désolé )

[PlaneteF]

Bonsoir et bonne année à toutes et à tous

Dans le domaine du "c'est pas parce que je n'y connais rien que je ne donne pas mon avis péremptoirement", un record vient d'être battu !

Cela me fait penser à :

https://fr.wikipedia.org/wiki/C%27es...rmer_sa_gueule



Cordialement

[invite51d17075]

Bonsoir et bonne année à toutes et à tous

A toi aussi , très sincèrement !

[Médiat]

Bonsoir PlaneteF

Pas totalement un hasard

Bonne année

[invite7f291776]

bjr,

Définition (une parmi d'autres possibles peut-être) : sqrt(2) est l'unique nombre qui multiplié par lui-même donne 2 : https://fr.wikipedia.org/wiki/Racine_carrée_de_deux

Il se trouve qu'il a des propriétés géométriques remarquables

[Médiat]

Définition (une parmi d'autres possibles peut-être) : sqrt(2) est l'unique nombre qui multiplié par lui-même donne 2 : https://fr.wikipedia.org/wiki/Racine_carrée_de_deux

Bravo, une (voire deux) erreur(s) de plus (en recopiant : )

[invite7f291776]

Vous manque "nombre réel positif" ou quoi ? En tout cas moi je vois sous le triangle du wikipedia : "L’hypoténuse d’un triangle rectangle isocèle de côté 1 vaut √2."

… très comme qui dirait "elliptique" aussi

Bah, "Il se trouve que l’hypoténuse d’un triangle rectangle isocèle de côté 1 vaut √2." ce serait mieux, je pense

[invite7b7f1ad0]

Vous manque "nombre réel positif" ou quoi ? En tout cas moi je vois sous le triangle du wikipedia : "L’hypoténuse d’un triangle rectangle isocèle de côté 1 vaut √2."

… très comme qui dirait "elliptique" aussi

Bah, "Il se trouve que l’hypoténuse d’un triangle rectangle isocèle de côté 1 vaut √2." ce serait mieux, je pense

Pourquoi ces digressions? Faut-il poser vous pas la question de savoir comment une idée se différencie de la réalité? La réalité est-elle, elle même, perceptible (peut-on vraiment se savoir exister)? De ces questions à l'approche mathématique il semble que l'on ne peut se contenter que de 2 voies.. la lecture du livre " L'Etonnant Modèle de Goebius " peut vous donner une perspective intéressante et troublante.
En attendant je ne peut que vous conseiller ces articles très riche:https://blogs.futura-sciences.com/lehning/?s=platon et https://blogs.futura-sciences.com/le...r-les-nombres/ en complément
@Mediat: il s'agissait bien d'imaginaire?

[Médiat]

Bonjour,

@Mediat: il s'agissait bien d'imaginaire?

Non, mais les mots "réels" et "positifs" sont essentiels, les oublier c'est prouver que l'on n'a pas compris.

Sur le blog que vous citez, il y a des phrases que je pourrais signer et d'autres que j'ai déjà écrites ici (sous une autre forme), par exemple

Ces nombres [les réels] n’existent pas plus dans la réalité que les autres

ou

Il n’existe pas d’axiomes « vrais », il existe des axiomes utiles.

[invite7b7f1ad0]

La formulation suivante est-elle admissible:
En maths, on ne peut pas parler de vrai au sens de la réalité physique mais il est nécessaire de formuler une cohérence au sein d'un système de conception rigoureusement abstraite.

[Médiat]

Oui, cela est parfaitement admissible, juste deux remarques :
1 ) L'usage du mot "vrai" est dangereux sauf si on parle de modèle et à la condition obligatoire que cela soit clairement dit (dans l'arithmétique de Peano, 1 + 0 =1 n'est pas vrai, mais démontrable, dans IN c'est vrai)
2) La cohérence (on dit consistance) est nécessaire, mais pour des théories importantes (ZF par exemple) on ne sait pas si elles sont consistantes ou non (on fait comme si)

[invite7b7f1ad0]

Merci de ces indications qui sont autant de pistes de travail, j'ai lu "Le rêve de la raison" dans la collection -Le monde est mathématique- durant l'été est je pense que je vais y remettre mon nez.
Avant d'envisager les maths, j'ai bien l'impression qu'il faille au préalable comprendre là ou l'être humain en est arrivé en matière de logique.

[invite51d17075]

bjr,

Avant d'envisager les maths, j'ai bien l'impression qu'il faille au préalable comprendre là ou l'être humain en est arrivé en matière de logique.

Mon ressenti est plutôt celui d'une boucle du type de la poule et de l'oeuf, mais je peux me tromper.
Personnellement, c'est plutôt en "pratiquant" les maths (à mon niveau ) que je pense mieux appréhender certaines logiques humaines.
Et si je présente les choses dans cette direction, c'est que les "logiques humaines" couvrent des champs bien plus larges.
Cdt

ps: je ne connais pas ce livre .... un avis ?

[invite7b7f1ad0]

Je me suis exprimé un peu de travers, je passe du temps en ce moment sur les notions fondamentales d'algèbre, j'ai trouvé des livres LEBOSSE-HEMERY...

Ce qui est expliqué plus haut m'a renvoyer vers des articles en particulier sur la théorie des modèles et en particulier cet article: https://fr.wikipedia.org/wiki/Struct...%C3%A9matique). Le risque est de confondre ce qui est purement du domaine mathématique avec une pratique de la raison plus large.
Dans ce sens, je cite une phrase que j'ai lu ce matin sur un site ; "Si on ne prend pas soin d'ordonner ses connaissances, plus on étudie, plus il y a matière à confusion et plus on régresse. L'étude des mathématiques n'est pas simplement cumulative, mais aussi structurée et relationnelle. La pensée floue et indifférenciée est ennemie de la culture. "
Le livre "Le rêve de la raison" fait parti de la collection "Le monde est mathématique" : https://images.math.cnrs.fr/Le-reve-de-la-raison.html
Les concepts et précautions présentés par Mediat m'ont fait repenser à ce livre.

[invite51d17075]

Ce qui est expliqué plus haut m'a renvoyer vers des articles en particulier sur la théorie des modèles et en particulier cet article: https://fr.wikipedia.org/wiki/Struct...%C3%A9matique). Le risque est de confondre ce qui est purement du domaine mathématique avec une pratique de la raison plus large.

Il me semble qu'avant le risque cité, il existe celui de ne pas bien saisir les concepts cités ( faute d'un background sufisant ) et donc de tomber dans "la pensée floue" que vous souhaitez éviter.
ici par exemple, le lien renvoie directement à la théorie des modèles , domaine qu'on approche éventuellement plusieurs années post Bac.
Ce n'est pas uniquement une question de capacité d'abstraction personnelle, et je ne peux préjuger de la votre.

ps :Je peux me tromper .... peut être est il possible de "sauter" directement à ce niveau, mais mon doute reste assez fort.

[invite7b7f1ad0]

Ce que je ne comprends pas c'est comment dans ce cas intégrer des éléments logiques adéquats dans l'apprentissage de certaines notions?
Pour l'exemple du mot vrai et de sa validité contextuelle en maths, ne faut-il pas avoir entendu parler de calcul des prédicats (entre autres)?
Au pire le fait d'aborder certaines notions peut apporter au moins la connaissance de ce que les choses ne sont pas, c'est faute d'être solide moins fragile qu'une appréhension uniquement basée sur des relations de causalité.
Le tout est de garder à l'esprit la différence entre appréhender et comprendre, l'autre variante est le renoncement à l’intellectualisation des connaissances (cas de la grande majorité de la population à mon avis).

[invite7f291776]

En maths, on ne peut pas parler de vrai au sens de la réalité physique mais il est nécessaire de formuler une cohérence au sein d'un système de conception rigoureusement abstraite.

La cohérence ou la logique sont des valeurs universelles, en ce sens que tout discours rationnel mais au sens de la rationalité humaine, ne peut pas s'en passer.

S'affranchir du rapport au réel physique, concret, de la réalité physique en somme pour discourir, cela peut s'avérer dangereux en effet des fous parfois, ont tout perdu et surtout comme qui dirait la "fonction du réel" ... sauf la logique !

Jusqu'à un certain degré d'abstraction, des pans entiers des mathématiques semblent directement décrire des réalités physiques sans que nul ne sache exactement pourquoi bah si ça marche pourquoi donc s'en priver ?

Mais au-delà, à des degrés d'abstraction plus élevés, les mathématiques semblent ou peuvent paraître, complètement autonomes, débranchées de la réalité physique, mais est-ce le cas réellement

Exemple qui ne comprend pas pourquoi l'aire d'un carré est a fois a et le volume d'un cube (a fois a) fois a, et jusqu'à 3 les racines carrées les "square roots" sont aisément représentables sur des schémas, des dessins.

Sqrt(2) cf plus haut, wikipedia consacre un article sur sqrt(3) mais ensuite plus rien sur sqrt(5), sqrt(7) sqrt(11) etc.

Donc sqrt(3) :

https://fr.wikipedia.org/wiki/Racine...3%A9e_de_trois :

La diagonale d'un cube de côté 1 mesure
√3.

La question au reste n'effleure pas trop les sciences physiques en général, qui trouvent simplement les mathématiques fort utiles et donc faire confiance aux mathématiques comme ça marche tout le monde est pour, voilà tout.

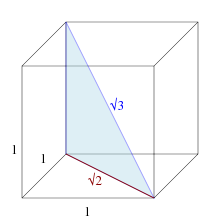
Bah, la triangulation https://fr.wikipedia.org/wiki/Triangulation , les calculs des probabilités etc., il se trouve que tiens le revoilà celui-là ça marche donc pourquoi donc s'en priver, ce serait trop bête

[invite51d17075]

Ce que je ne comprends pas c'est comment dans ce cas intégrer des éléments logiques adéquats dans l'apprentissage de certaines notions?
Pour l'exemple du mot vrai et de sa validité contextuelle en maths, ne faut-il pas avoir entendu parler de calcul des prédicats (entre autres)?
Au pire le fait d'aborder certaines notions peut apporter au moins la connaissance de ce que les choses ne sont pas, c'est faute d'être solide moins fragile qu'une appréhension uniquement basée sur des relations de causalité.
Le tout est de garder à l'esprit la différence entre appréhender et comprendre, l'autre variante est le renoncement à l’intellectualisation des connaissances (cas de la grande majorité de la population à mon avis).

peut être "attaquer" le sujet via l'histoire de la logique mathématique:
https://fr.wikipedia.org/wiki/Logique_math%C3%A9matique
puis creuser ensuite certains sous sujets comme la théorie des ensembles.
je devrais m'exprimer au conditionnel, car je ne suis pas le plus compétent ici ( de loin ) pour proposer une démarche ad-hoc.
Cdt

[invite7b7f1ad0]

peut être "attaquer" le sujet via l'histoire de la logique mathématique:
https://fr.wikipedia.org/wiki/Logique_math%C3%A9matique
puis creuser ensuite certains sous sujets comme la théorie des ensembles.
je devrais m'exprimer au conditionnel, car je ne suis pas le plus compétent ici ( de loin ) pour proposer une démarche ad-hoc.
Cdt

C'est bien le bon schémas à mon avis aussi, la théorie des ensembles ouvre cependant les vannes d'un trop plein d'idées pour moi: j'ai l'impression de partir dans tout les sens, une théorie des suites m'aurait plus convenu mais je m'y met bien plus sérieusement désormais grâce aux lectures que j'ai faites ici même.
Je ne sais pas pourquoi ces questions m'occupent tellement l'esprit, ce n'est pas d'aujourd'hui et je pense avoir développé des schémas de raisonnement au sujet des nombres durant toute mon existence; c'est seulement maintenant que je découvre la richesse de ce qui a été fait. Je n'ai pas de grandes ambitions que de la curiosité cela me rend patient et je progresse quand même.

[Médiat]

la théorie des ensembles

Méfiez vous de la théorie des ensembles, elle a le défaut de paraître simple (elle n'est pas horriblement compliquée, mais on risque de comprendre de travers si on se fie trop à son intuition)

[invite7b7f1ad0]

Méfiez vous de la théorie des ensembles, elle a le défaut de paraître simple (elle n'est pas horriblement compliquée, mais on risque de comprendre de travers si on se fie trop à son intuition)

Un peu de poèsie:
Elle me semble être comme une rivière au fond d'un canyon, envoutante par le bleue émanant de sa profondeur et son apparence calme et régulière mais j'ai compris que le courant y était par contre fort et que pour y naviguer il fallait savoir lire dans les reflets des quelques vagues émergentes.. passer à côté serait traverser le canyon sans le voir car une fois le canoé retourné le navigateur devenu nageur n'a plus de hauteur pour savoir ou il est.

Je suis toujours sur la berge et j'observe, je me méfie

Mais bon va falloir que je largue les amarres un jour, il n'y a qu'une et une seule traversée.

[invite7f291776]

Bonjour,

La diagonale d'un cube de côté 1 mesure
√3.

N’est-ce pas un brin drôle encore qu’il ne faille pas rire sans raisons, cette définition mathématique qui parle de « mesure » pour définir un calcul mathématique ?

Surtout cela montre la confiance que les sciences physiques accordent aux calculs mathématiques et justement c’est cette confiance qui est en question. Elle n’est sans doute pas aveugle et dans tous les cas elle n’est pas feinte en effet celle-là. Des raisons à cela existent forcément en effet rien ne sort de rien et encore moins du « néant ».

D’autres exemples abondent dans ce sens et dans tous les domaines des sciences physiques et même sociales :

1)

En géométrie et trigonométrie, la triangulation est une technique permettant de déterminer la position d'un point en mesurant les angles entre ce point et d'autres points de référence dont la position est connue, et ceci plutôt que de mesurer directement la distance entre les points. Ce point peut être considéré comme étant le troisième sommet d'un triangle dont on connaît deux angles et la longueur d'un côté. ( https://fr.wikipedia.org/wiki/Triangulation )

2)

Quand Le Verrier calcule la position de la planète Neptune, non encore découverte concrètement, ses calculs sont des pré-mesures physiques mais des « mesures » mathématiques. Ensuite euréka des appareils d’observation ont été pointés dans la direction indiquée par les calculs-mesures de Le Verrier et donc en sept 1846, la découverte mais réelle, physique ou concrète cette fois, de la planète a été confirmée, validée par la communauté scientifique

( https://fr.wikipedia.org/wiki/Découverte_de_Neptune )

3)

En quantique une « mesure » est un calcul ou une opération mathématique et donc là encore et peut-être plus que nulle part ailleurs, calculer c’est mesurer :

( https://fr.wikipedia.org/wiki/Problè...sure_quantique )

[Deedee81]

Salut,

N’est-ce pas un brin drôle encore qu’il ne faille pas rire sans raisons, cette définition mathématique qui parle de « mesure » pour définir un calcul mathématique ?

En mathématique, la théorie de la mesure ça existe : https://fr.wikipedia.org/wiki/Th%C3%A9orie_de_la_mesure

Et ça n'a rien à voir avec la mesure en physique.

Je vais t'apprend un scoop qui va bouleverser ta vie : les mots ont parfois plusieurs significations.
Et qui sait, ça évitera peut-être des messages comme celui que tu viens de poster et où tu fais cette confusion (désolé de le dire mais c'est n'importe quoi).

[invite7f291776]

Soit mais qu’a « la mesure de Lebesgue » à voir avec un triangle dessiné, concret, « en chair et en os » si j’ose dire ?

La notion mathématique d’« espace mesuré » a-t-elle à voir avec un triangle dans un cube physique, concret, dessiné sur une feuille de papier ou qui apparaît sur l'écran d’un ordinateur ?

Donc perso quand je lis sur wikipedia, « La diagonale d'un cube de côté 1 mesure √3. » là perso, je mets un peu de temps à comprendre quand même !

Et les calculs de Le Verrier et la technique (tiens c'est assez symptomatique de parler de technique à cet endroit je trouve) de triangulation utilisée en physique pour mesurer-calculer des choses et d'autres genre des distances entre des astres etc. … qu'est-ce donc que tout ceci a à voir avec la notion mathématique d’« espace mesuré » ?

[invite51d17075]

tu t'enfonces là !
qu'y a t-il à comprendre à part que les maths et la physique ( surtout celles du collège et du lycée ) emploient des termes du langage courant pour être facilement compréhensibles ?
et c'est aussi le cas dans le cas de concepts ou théories plus "pointus"..( sauf que les mots y ont leur propre sens ).

cela fait plusieurs interventions du même ordre de ta part.
en supposant que ce ne soit pas du trollage ( qui serait malvenu ), il y a alors de l'aveuglement ou bien une incompréhension profonde, ou bien ....je ne sais pas.

[Deedee81]

tu t'enfonces là !
qu'y a t-il à comprendre à part que les maths et la physique ( surtout celles du collège et du lycée ) emploient des termes du langage courant pour être facilement compréhensibles ?
et c'est aussi le cas dans le cas de concepts ou théories plus "pointus"..( sauf que les mots y ont leur propre sens ).

Sans compter que la physique utilise des outils mathématiques, avec toutes les règles d'usages/de limitation/de précision/etc... appropriées. Mais pas l'inverse.

[invite046e427d]

Bonjour,

...

En mathématiques, peut-être que la physique peut être vue comme une aide à des démarches constructivistes c'est-à-dire un pied dans le réel et un dans l'abstrait.
Cdt.

[Deedee81]

Précision sur ma dernière remarque.

Il est vrai que les mathématiques se sont parfois inspirées du "monde réel" par exemple avec les nombres naturels pour compter.
Mais ça reste limité. Et ce n'est même pas le cas de la mesure car la théorie de la mesure ne prend que trèèèèèès indirectement inspiration de la mesure des longueurs, aires,....
C'est en fait venu de besoin dans la théorie de l'intégration.
#################

[mh34]

aygline si vous n'avez pas encore compris que votre participation à ce fil s'arrête là je vous l'apprends.
Au prochain message, vous prendrez des vacances.