Bonjour à tous,
Dans un cours sur les nombres complexes, on nous introduit toujours le fameux nombre i en précisant que i²=-1. Mais est-ce vraiment une hypothèse à la base de?
En général, plutôt que de considérercomme l'ensemble des nombres s'écrivant de la forme a+ib avec
, je préfère le rapprocher de
.
Dans ce cas, i=(0;1), et on devrait avoir i²=(-1;0), mais pourquoi est-ce le cas ?
Quelqu'un pourrait-il m'éclairer ?
Merci d'avance
Phys2
-----




 .
.
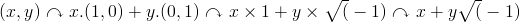
 Un lien ?
Un lien ?

