travail du champ de gravitation en relativité générale.

[mach3]

Pouvons-nous dire pour autant que Ev = Eu * Yw ?

Je ne sais pas répondre pour l'instant, je n'ai pas abordé l'aspect énergétique (et déjà rien qu'à y réfléchir dans ma tête je trouve ça assez bordélique, beaucoup de conflits entre l'énergie mécanique classique, l'énergie de la relativité restreinte qui n'est que masse+cinétique si il n'y a pas de champ d'interaction et l'énergie de la relativité générale, qui localement doit correspondre à celle de la restreinte, mais globalement doit reproduire un truc qui colle avec l'énergie mécanique classique en champ faible)

Quel sens physique donnerais-tu à L?

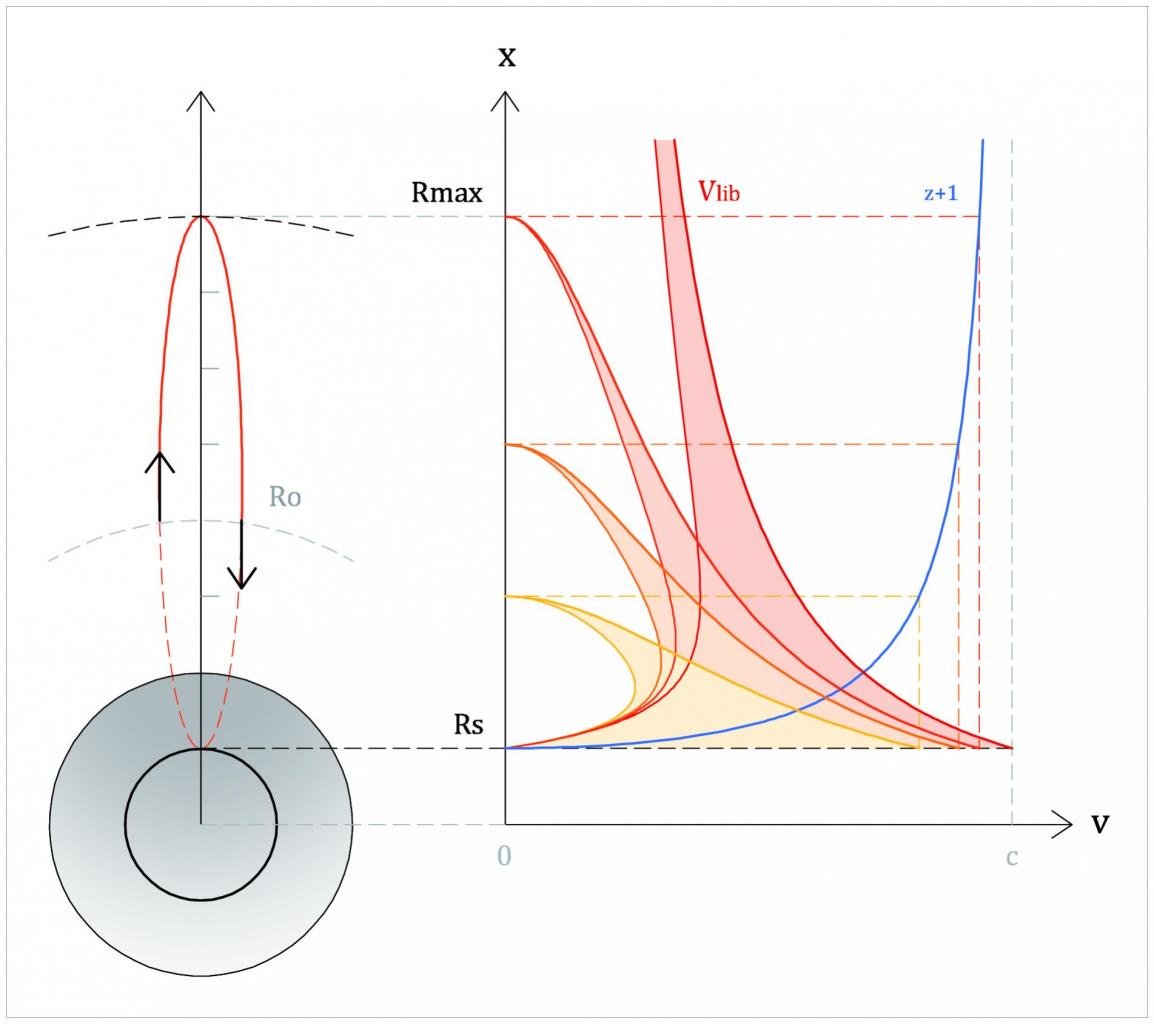
Aucun a priori... c'est juste un bête paramètre pour identifier les géodésiques passant par un même évènement (il en faut 3 au total quand on est en 3+1, un seul suffit en 1+1), comme on peut en inventer des tas d'autres. C'est pareil pour K, pas de sens physique a priori. Le fait qu'on puisse dans certains particuliers (chute libre culminante) relier L ou K à la valeur de la culmination ne dit rien sur L ou K en général (en fait peu importe la forme du "machin" qui identifie, K ou L ou N... du moment qu'il est constant le long de la géodésique, si c'est une géodésique avec culmination, on peut forcément y relier rmax).
Devant le fait que l'expression de dr/dt satisfait l'équation des géodésiques, et qu'en plus elle décrit l'ensemble des géodésiques, le sens physique de K ou L n'est pas d'une importance capitale.

Les K négatifs sont à mon sens les «débiles», car avec cette définition de K ils n’ont aucun sens.*

un cas mathématiquement proche est la position du "punctum remotum" en fonction de la vergence de l'oeil au repos. Pour un oeil normal (image nette à l'infini au repos, possibilité de voir net au minimum à une dizaine de centimètres en accommodant), le punctum remotum est à l'infini, pour un oeil myope (image nette à une distance finie au repos, impossible de voir net à l'infini, possibilité de voir net au minimum à quelques centimètres en accommodant), le punctum remotum est à une distance finie, pour un oeil hypermétrope (pas d'image nette au repos, mais possibilité de voir net à l'infini et possibilité de voir net au minimum à quelques dizaines de centimètre ou quelques mètres en accommodant), le punctum remotum est à une distance négative (derrière l'oeil). En fait un objet virtuel situé derrière formerait une image réelle sur la rétine de l'oeil hypermétrope au repos, d'ailleurs c'est ce que fabrique une lentille de lunette pour hypermétrope à partir d'un objet réel (se référer à des cours d'optique géométrique pour comprendre tout ça). On a une grandeur qui varie continument de l'oeil myope à l'oeil hypermétrope en passant par l'oeil normal, et pendant qu'elle varie, le punctum remotum s'éloigne, diverge, puis "revient par derrière", dans les négatifs, un peu comme -1/x quand on passe x=0 en augmentant x... Dans ce sens, plus loin que +infini, c'est -infini et les nombres négatifs. Même chose avec la température, on peut définir dans des cas très particuliers, des températures absolues négatives, qui sont en fait plus chaudes qu'une température absolue arbitrairement positive (il faut se rappeler que la température est liée aux statistiques de populations des états et qu'une inversion de population donne la température opposée), en fait il faut travailler avec 1/T pour que ça fasse sens.
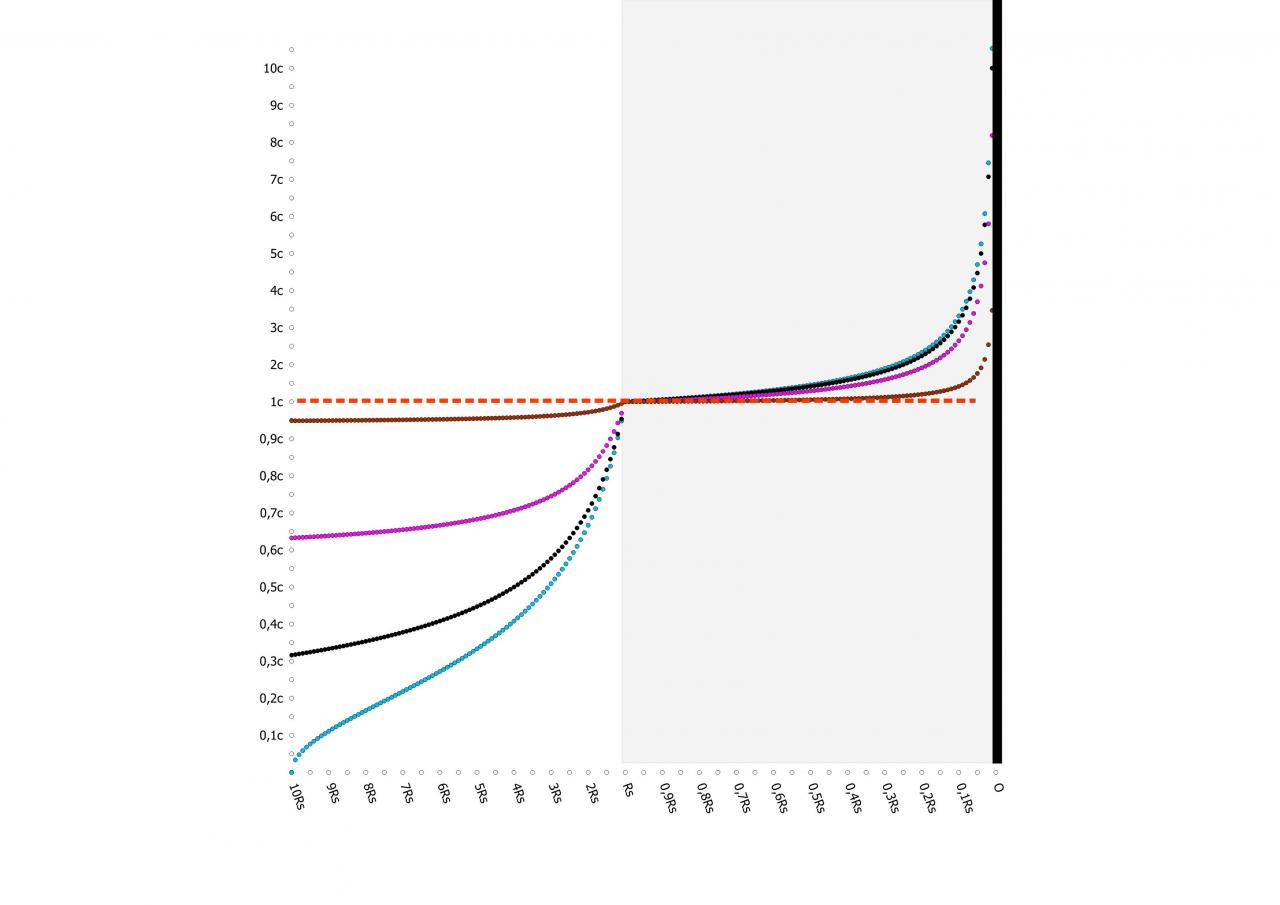
Du coup, si rmax est négatif, cela signifie grosso-modo que le dr/dt s'annule pour r "plus grand que l'infini", "donc" négatif. C'est plus logique en réfléchissant avec 1/r qui doit devenir plus petit que 0, donc négatif...
Mais bon, peu importe, comme déjà dit, K n'est qu'un paramètre et qu'il soit en relation avec rmax dans le cas avec culmination ne doit pas empêcher de s'en servir dans les autres cas où rmax n'a pas de sens.

- Pour 1/Rs<K<oo on a 0<Rmax<Rs, soit des objets qui chutent depuis l’intérieur du TN. A nouveau, ce qui est de genre espace en (r;t) de Schw devient de genre temps en region II.

J'ai l'intuition (et je compte bien le démontrer) qu'il s'agit de géodésiques de genre espace qui viennent de l'infini de la région I (r infini donc), qui plongent sous l'horizon, "descendent" jusqu'à ce que r=1/K, puis "remontent", ressortent par l'autre horizon et partent vers l'infini de la région III. Prends une géodésique de chute libre avec culmination qui fait IV-I-II dans un Kruskal, et fait la tourner de 90° autour du centre X=T=0, ça donne un truc qui fait I-II-III (ou I-IV-III, ça dépend du signe de dr/dt) avec un r minimal (au lieu de maximal) qui doit avoir l'allure d'une telle géodésique de genre espace (et peut-être pas seulement l'allure, si ça se trouve c'est directement la géodésique, ça ce serait marrant).

peux tu preciser le changement de variable de K vers L stp ? mci

On pose (oui, oui, c'est du bricolage sur mesure pour avoir le changement de genre quand L change de signe).

m@ch3
-----

[Zefram Cochrane]

Bonjour,

Je ne sais pas répondre pour l'instant, je n'ai pas abordé l'aspect énergétique (et déjà rien qu'à y réfléchir dans ma tête je trouve ça assez bordélique, beaucoup de conflits entre l'énergie mécanique classique, l'énergie de la relativité restreinte qui n'est que masse+cinétique si il n'y a pas de champ d'interaction et l'énergie de la relativité générale, qui localement doit correspondre à celle de la restreinte, mais globalement doit reproduire un truc qui colle avec l'énergie mécanique classique en champ faible)

Voici ce que j'ai fait ( j'espère pouvoir aider) :
Un développement limité de Yu en Ro et Yv en R donne :


Le développement limité de Yw donne pour R proche de Ro :

En négligeant
j'obtiens :

cela nous donne que :

en négligeant les produits et :

on multiplie le tout par et on remplace Rs par nous obtenons :

c'est-à-dire :

pour les champs faibles ( je te laisses juge de la pertinence des calculs )

J'ai l'intuition (et je compte bien le démontrer) qu'il s'agit de géodésiques de genre espace qui viennent de l'infini de la région I (r infini donc), qui plongent sous l'horizon, "descendent" jusqu'à ce que r=1/K, puis "remontent", ressortent par l'autre horizon et partent vers l'infini de la région III. Prends une géodésique de chute libre avec culmination qui fait IV-I-II dans un Kruskal, et fait la tourner de 90° autour du centre X=T=0, ça donne un truc qui fait I-II-III (ou I-IV-III, ça dépend du signe de dr/dt) avec un r minimal (au lieu de maximal) qui doit avoir l'allure d'une telle géodésique de genre espace (et peut-être pas seulement l'allure, si ça se trouve c'est directement la géodésique, ça ce serait marrant).

Oui ça serait très drôle, je comptais justement vous proposer de passer à la vitesse supérieure à c sitôt ces histoires d'énergie réglées

[mach3]

OK, je vais voir si j'arrive à retomber là-dessus. Si une particule en chute libre de masse m et de 4-impulsion P passe devant un immobile de Schwarzschild en r_0 et de 4-vitesse U_0, il mesure l'énergie suivante pour la particule :



Même chose, mais devant un autre immobile, en r_1 :



Enfin, devant un immobile situé arbitrairement loin (on fait diverger r) :



L'énergie de la particule change. L'énergie ne semble pas conservée. Normal, la RG ne fait que de la conservation locale : la 4-impulsion est bien transportée identique à elle même le long de la géodésique de la particule en chute, elle ne change pas, mais l' "angle" que font les immobile de Schwarzschild avec elle ne cesse de changer et donc l'énergie (qui dépend du cosh de cet "angle") change. Si on veut réintroduire de force une conservation de l'énergie, il faut ajouter un terme. On aura :





tel que

Il faut maintenant trouver la forme que peut prendre la fonction Ep.
On arrive sauf erreur à :


A suivre...

m@ch3

[Zefram Cochrane]

Voo n'est-il pas nul?
cela donnerait alors

soit

???
on aboutit à un Ep de la forme :

[Zefram Cochrane]

annule le message précédent SVP
Voo n'est-il pas nul?
cela donnerait alors

soit

???

[mach3]

On peut prendre l'énergie potentiel nulle à l'infini, mais ça relève d'une convention, au moins en mécanique classique, on peut très bien la prendre nul au niveau du sol (par exemple quand on utilise mgh avec h la hauteur par rapport sol). Je ne sais pas ce qu'il en est en RG. Si on considère une différence d'énergie potentielle on ne risque pas de se tromper.
En tout cas pour l'instant ça ne sent pas bon, car l'énergie potentielle dépend de L (c'est à dire que deux chuteurs libres, de mêmes masses, de vitesses différentes mais de même r aurait des énergies potentielles différentes), alors qu'elle ne le devrait pas. J'ai dû louper quelque chose.

m@ch3

[mach3]

En tout cas pour l'instant ça ne sent pas bon, car l'énergie potentielle dépend de L (c'est à dire que deux chuteurs libres, de mêmes masses, de vitesses différentes mais de même r aurait des énergies potentielles différentes), alors qu'elle ne le devrait pas. J'ai dû louper quelque chose.

Pas sûr qu'il faille considérer l'énergie telle que mesurée par un immobile. Les énergies mesurées par différents immobiles à différents r le long d'une chute ne sont peut-être pas comparables du fait qu'ils ne sont pas au même r et que leurs horloges ne peuvent être synchrones. Il faut peut-être plutôt considérer ce que voit un observateur de r fixe, c'est à dire une mesure de vitesse entachée du redshift gravitationnel. A tester.

m@ch3

[Zefram Cochrane]

Ce serait un gros problème s'il n'y avait pas de définition objective de l'énergie potentielle de gravitation?
Quand j'ai posé Ev = Eu*Yw ma question était que devenait cette énergie potentielle de gravitation dans le contexte?
le fait d'avoir L qui se balade dans les formule démontrerait peut-être le caractère subjectif de ce concept?
Si la RG ne voit plus la gravitation comme une force, ne pas pouvoir définir objectivement une énergie potentielle de gravitation n'est peut-être par rédhibitoire si le concept d'énergie potentielle de gravitation et celui de force ne peuvent être dissociés?

[mach3]

Ce serait un gros problème s'il n'y avait pas de définition objective de l'énergie potentielle de gravitation?

Le problème est qu'il faut retrouver Newton en champ faible, et avec L qui se ballade, ça ne semble marcher que pour L=-2M (chute libre à Vlib), ce qui ne me semble pas normal. La démarche que j'ai suivie ne doit pas être la bonne pour faire ça. Je verrais si j'ai le temps de voir comment c'est fait dans la littérature.

m@ch3

[Zefram Cochrane]

moi aussi je jetterai un oeuil dans ma bibliothèque.
@+

[mach3]

Petit essai au culot. La 4-vitesse a pour composante
Or la 4-vitesse c'est , donc



Aller, osons.




est constant et dépend de la géodésique (fonction de L). On note que si L=-2M (chute libre à Vlib), il s'annule, ça ressemble drôlement à de l'énergie mécanique classique avec potentiel nul à l'infini
ressemble beaucoup à de l'énergie cinétique.
Il reste est l'opposé de l'énergie potentiel classique, ça fait Ec = E - Ep. Ca se tient...

A creuser.

m@ch3

[Mailou75]

Salut,

J'ai l'intuition (et je compte bien le démontrer) qu'il s'agit de géodésiques de genre espace qui viennent de l'infini de la région I (r infini donc), qui plongent sous l'horizon, "descendent" jusqu'à ce que r=1/K, puis "remontent", ressortent par l'autre horizon et partent vers l'infini de la région III. Prends une géodésique de chute libre avec culmination qui fait IV-I-II dans un Kruskal, et fait la tourner de 90° autour du centre X=T=0, ça donne un truc qui fait I-II-III (ou I-IV-III, ça dépend du signe de dr/dt) avec un r minimal (au lieu de maximal) qui doit avoir l'allure d'une telle géodésique de genre espace (et peut-être pas seulement l'allure, si ça se trouve c'est directement la géodésique, ça ce serait marrant).

Je pourrais regarder ça à la rentrée, je te dirais

On pose (oui, oui, c'est du bricolage sur mesure pour avoir le changement de genre quand L change de signe).

Ce n’était pas pour critiquer (je vois bien l’avantage) juste que je suis une grosse feignasse... j’avoue préférer K pour l’instant, même si c’est une barrière conceptuelle.

En tout cas pour l'instant ça ne sent pas bon, car l'énergie potentielle dépend de L (c'est à dire que deux chuteurs libres, de mêmes masses, de vitesses différentes mais de même r aurait des énergies potentielles différentes), alors qu'elle ne le devrait pas. J'ai dû louper quelque chose.

Sur ce point je rejoins Zef, il n’est peut être pas judicieux de chercher à reproduire la gravité classique. A priori le potentiel serait le même qu’en classique, la «courbure» négative à l’extérieur d’un astre : -GM/r devient 1/z+1. La courbe est toujours la même dans les cas classiques chez Newton et Einstein, seules les unités changent, avec le sens...

Mais le sujet tel qu’il apparait aujourd’hui semble plus simple. Un objet part de Rmax (pouvant être l’infini) avec une énergie E (ou Y.E si sa vitesse de départ n’est pas nulle) ensuite il transforme au fur et à mesure de sa chute des intervalles de potentiel (delta z+1) en un Y’ supplémentaire. Sa vitesse locale de chute est donc un beta B correspondant à Y*Y’. Ex : pour des vitesses de chute successives u, v puis w avec une vitesse initiale nulle la constante est la masse E = Eu/Yu = Ev/Yv = Ew/Yw etc... (pour une vitesse intiale non nulle, la constante est Y.E). Il n’y a donc pas nécessité à recourir à une énergie «potentielle» puisque la différence de potentiel est contenue dans le Y(r) local (?)

Je verrais si j'ai le temps de voir comment c'est fait dans la littérature.

Un artilcle de Mizony http://math.univ-lyon1.fr/~mizony/metriquePainleve.pdf mais y’en a des meilleurs avec des Kruskal, je ne retrouve pas... comme il parle de Painlevé t’auras peut être dTau (ça m’interesse pour mes petits points ^^). NB : pas de garantie sur l’auteur d’après ce que j’ai compris...

Bon courage A +

[Mailou75]

Re,

Je pourrais regarder ça à la rentrée, je te dirais

En fait non, je vais manquer de données, il me faudrait des trajectoires et un temps propre

Du coup ça s’intègre ce truc pour avoir un courbe t(r) chez Schw ?
(la formule «généralisée» avec K ou L risque de piquer les yeux, quand on connait la restreinte...)

Et celle là ? si elle est juste, pour la version Tau(r) chez Newton+ et pour pouvoir ponctuer Schw avec le temps propre. (Ensuite je me demerde pour Kruskal)

Avec ça je pourrais te dire si ça semble coller (et comparaison avec cas classique, je dois avoir la formule dans un coin). Sans, je ne sais pas faire, j’ai bien un plugin donné par Lansberg pour qu’Excel fasse des intégrales mais je ne sais pas m’en servir (boulet...).

Le mec ne fout rien et en plus il demande la suite, manque pas d’air !

[Zefram Cochrane]

Bonjour,
Si l'objectif de l'approximation des champs faibles correspond à celui affiché ici :
https://fr.wikipedia.org/wiki/Approx...champs_faibles

Je ne sais pas répondre pour l'instant, je n'ai pas abordé l'aspect énergétique (et déjà rien qu'à y réfléchir dans ma tête je trouve ça assez bordélique, beaucoup de conflits entre l'énergie mécanique classique, l'énergie de la relativité restreinte qui n'est que masse+cinétique si il n'y a pas de champ d'interaction et l'énergie de la relativité générale, qui localement doit correspondre à celle de la restreinte, mais globalement doit reproduire un truc qui colle avec l'énergie mécanique classique en champ faible)

Je pense qu'il faut se limiter aux vitesses et valeur de champ de gravitation ou la mécanique newtonienne est une bonne approximation.
C'est-à-dire u<v<<c et Ro>R>>2M.
D'où le message 32
https://forums.futura-sciences.com/d...ml#post6409752
ce que nous dit la formule
c'est qu'il s'appoximatise en (1-2M/Ro)(1+2M/R)
et que Eo.Yu s'appximatise en et Eo.Yv en
donc on aboutit à ce que la formule
si on considère que
on a
Donc pour moi la relation Ev = Eu * Yw colle avec l'approximation des champs faibles pour peu qu'on se limite à des valeurs de vitesse et de potentiels de gravitation pour lesquels cette approximation est possible.
Est-ce suffisant?

[mach3]

Salut.

Alors, mon petit doigt m'a dit (enfin, je dis mon petit doigt, il pèse quand même dans les 3kg et 1300 pages le petit doigt, hein...) :
,
avec
dans le cas radial (le moment cinétique vient un peu compliquer l'expression dans le cas non radial).
Pas été plus loin (je veux encore réfléchir un peu par moi-même, on va dire que c'est un indice).
Pas encore eu le temps de tout mettre à plat, mais il semblerait bien que le E de cette expression n'est pas l'énergie mesurée par les immobiles de Schwarzschild successifs que le chuteur croise contrairement à ce que j'essaie de faire. Ce serait probablement celle mesurée par l'observateur à l'infini (donc avec un redshift), ou encore par un immobile de Schwarzschild utilisant t comme temps et non son temps propre, ce qui a pour effet de modifier sa façon de mesurer l'énergie (ou encore que le 4-vecteur sur lequel on projette n'est pas une 4-vitesse, mais un 4-vecteur avec (1,0) comme coordonnées), mais je n'ai pas eu le temps de le montrer, c'est du travail de tête pour l'instant, sans griffonages sur un coin de table.
J'essaierai de débroussailler ça dans la semaine.

m@ch3

[mach3]

,
avec
dans le cas radial

Donc ça nous donne :




Or, on a , la 4-vitesse, avec :




Donc on a :





Soit , la 4-impulsion et un 4-vecteur, on a :




On obtient donc ce "E", par projection de la 4-impulsion sur un 4-vecteur tangent à un immobile de Schwarzschild mais qui n'est pas sa 4-vitesse. En effet, la norme de ce 4-vecteur est et non 1.

m@ch3

[mach3]

Suite.

On a donc :



Or, on a posé que la 4-vitesse a pour composante ,












L est en fait lié à l'inverse du carré de l'énergie E. On peut réécrire les composantes de la 4-vitesse :





La chute libre est donc caractérisée par :


et surtout :


L'étiquette qui désigne les géodésiques est cette fois E² et il a du sens physique. On a du genre temps si E²>0, du genre espace si E²<0, du genre nul si E infini et/ou m=0. On note, pour le genre temps, que si E<m, on a culmination, E=m, vitesse nulle à l'infini, E>m, vitesse non nulle à l'infini.

Reste à bien comprendre la raison qui fait choisir le 4-vecteur V : (1,0) pour la projection.

m@ch3

[Zefram Cochrane]

Bonjour,
Dans le cadre d'une chute radiale, la métrique de Schwarzschild peut s'écrit :

où encore :

Je reprends la formule 43 du cours d'Andy Caroll : : http://www-cosmosaf.iap.fr/MIT-RG-27.htm
et je la combine avec la tienne :
J'obtiens:

.............................. ..............

.


.............................. ..............

Si tu traces (dr/dt) et (dr\d\tau) tu obtiendrais la figure suivante (comme Mailou) :

https://forums.futura-sciences.com/a...ml#post4404033
Ce schéma montre que les (dr/dt) convergent vers 0 quand r->2M et que les (dr/d\tau) abordent 2M avec une valeur<c
je calcule ensuite la célérité :

La célérité, c'est comme les épinards: au début on n’aime pas mais après une bouchée pour maman et une bouchée pour papa on s’y fait
donc:

.

c’est-à-dire:

:nous tenons le bon bout

Zefram

[mach3]

Il faut maintenant "oublier" L et K, qui n'étaient que des béquilles et travailler seulement avec E/m (qui est souvent noté ). D'autant plus que pour passer à la suite, c'est à dire le non radial (un jour ou l'autre, on y viendra), il y aura le moment cinétique L, et donc une collision de notation.

m@ch3

[Mailou75]

Salut,

L/Rs, E/m ou 1-Rs.K tout ça c’est kif kif, aucun ne semble avoir plus de sens physique. Le seul que j’entrevois est le «carré de la vitesse coordonnée de la lumière à l’altitude de départ chez Schw» mais est ce vraiment cela qu’il faut comprendre ? Quoi qu’il en soit, j’ai tenté hier soir les intégrales pour les trajectoires et apparemment il y a une grande différence entre L>Rs et L<Rs cad entre les chutes sans vitesse initiale depuis Rmax (pouvant être infini) et tout le reste. En fait les vitesses non nulles à l’infini ont la même équation que les genre espace alors qu’on aimerait trouver une distinction entre genre espace et genre temps. Ceci n’est pas pour me convaincre que les trajectoires avec vitesse non nulle à l’infini sont réelles. Les maths nous disent qu’elles appartiennent à des cas non réels.

Pour tout le domaine d’étude avec lequel des comparaisons chiffrées sont possibles, les formules fonctionnent (je remplace K par 1/Rmax). Pour le reste je doute qu’on ait des références... en tout cas la distinction réel/irréel semble se situer ailleurs qu’entre genre espace et genre temps. Je ne sais pas trop qu’en penser, je suis en train de faire marche arrière pour en revenir à mes premières impressions : les trajectoires que l’on tente d’étudier n’appartiennent pas plus à Schw que des genre espace.

[mach3]

Salut,

L/Rs, E/m ou 1-Rs.K tout ça c’est kif kif, aucun ne semble avoir plus de sens physique.

Ah ben si, E (et E/m) a un sens physique en connexion avec l'énergie mécanique classique. Tout comme elle, il s'agit d'une constante du mouvement. Dans le cas radial elle caractérise entièrement un mouvement libre (ie une géodésique, à une translation temporelle près) et elle ne varie pas au cours du mouvement libre.

Quoi qu’il en soit, j’ai tenté hier soir les intégrales pour les trajectoires et apparemment il y a une grande différence entre L>Rs et L<Rs cad entre les chutes sans vitesse initiale depuis Rmax (pouvant être infini) et tout le reste. En fait les vitesses non nulles à l’infini ont la même équation que les genre espace alors qu’on aimerait trouver une distinction entre genre espace et genre temps.

Dans le cas de Minkowski, une géodésique, quelque soit son genre, est d'équation avec et des constantes. La distinction entre genre espace, nul ou temps n'est pas au niveau de l'expression de la géodésique, mais au niveau du genre du 4-vecteur tangent u que cela engendre, qui aura comme composantes et donc comme carré scalaire :

On voit tout suite que le genre nul correspond à et qu'on est en genre temps pour une valeur strictement inférieure en valeur absolue à 1 et de genre espace pour une valeur strictement supérieure. Avec une seule expression, on passe continument par tous les genres en faisant varier

Pas étonnant que l'équation décrivant une géodésique radiale de Schwarzschild ne présente pas de distinction a priori en fonction du genre de la géodésique... C'est le genre du 4-vecteur tangent qui fera la distinction :

Le genre nul correspond à

Ceci n’est pas pour me convaincre que les trajectoires avec vitesse non nulle à l’infini sont réelles. Les maths nous disent qu’elles appartiennent à des cas non réels.

ben non, tant que c'est du genre temps, ça peut être la géodésique d'une masse test.

Par ailleurs ces géodésiques là sont fidèles en champ faible aux trajectoires avec V>Vlib en mécanique classique, elles correspondent totalement à quelque chose de réel. Et pour sortir du cas purement radial, c'est avec une géodésique de genre nul (donc dr/dt=1 quand r tend vers l'infini) qu'on prédit correctement la déviation de la lumière par le Soleil. Je vois mal comment faire moins réel.

La géométrie de Schwarzschild décrit plutôt bien les mouvements dans le système solaire en première approximation, c'est à dire Soleil comme masse centrale immobile et planète ou autre objet de masse négligeable (et mieux que les lois de Kepler qui sont aussi formulées dans cette approximation M>>m), et les mouvements sur des trajectoires hyperboliques (V>Vlib) font partie de cette description (tout comme avec Kepler).

m@ch3

[Zefram Cochrane]

Bonjour,
Je ne suis pas au clair avec cette 4-vitesse ?

Pour moi la 4-vitesse correspondant à la vitesse locale*:

a pour composante;

ce qui est conforme avec la formule du facteur de Lorentz :

avec
le chuteur est un photon
le chuteur est un mobile chutant depuis une altitude Ro < oo avec une vitesse initiale nulle.
le chuteur est un mobile chutant à Vlib
le chuteur est un mobile chutant à une vitesse > Vlib
On le comprend mieux sous cette forme.

où Eo est l’énergie que le mobile aurait à l’oo; ce qui donne pour la 4-vitesse:

Pour un mobile chutant depuis Ro avec une vitesse supérieure ou égale à 0 (*)
Ce que nous dit cette forme c’est que si u est la Vlib en Ro et et w est la vlib en R:
alors

Avec une énergie en R de
.
Je trouve que cette formule correspond bien à un cas très réel.
Cordialement,
Zefram
(*)mais je préfère rester pour ma part sur des valeurs de allant de 0 à l’oo si on veut aborder par la suite les valeur de négatives.

[mach3]

Bonjour,
Je ne suis pas au clair avec cette 4-vitesse ?

Par définition, pour une 4-vitesse U, on a g(U,U)=1 (en signature +--- avec c=1). Si on est coordonnées de Schwarzschild (t,r), la métrique est :


La 4-vitesse est :
, ce que je notais : , notation qui est inféodée au choix du système de coordonnées (t,r de Schwarzschild, implicitement)

on a donc :


Si on est dans des coordonnées modifiées, par exemple (t',r') telles que et , la métrique est, en :


La 4-vitesse est :
et on la note alors, dans ce système de coordonnées là , l'expression des coordonnées d'un vecteurs dépend du système de coordonnées.

on a donc :


On peut vérifier que les deux g(U,U) sont bien les mêmes (il suffit de remplacer dt' et dr' par leurs expressions en fonction de dt et dr).

En particulier, en r_0, on a :



la métrique possède localement l'expression de celle de Minkowski en coordonnées de Lorentz 1+1.

Je reviendrais sur la suite plus tard.

m@ch3

[mach3]

avec
le chuteur est un photon
le chuteur est un mobile chutant depuis une altitude Ro < oo avec une vitesse initiale nulle.
le chuteur est un mobile chutant à Vlib
le chuteur est un mobile chutant à une vitesse > Vlib

Attention, pour le photon, c'est (la masse est nulle, E/m diverge). Le cas n'existe pas en genre temps dans la région I.
Il semble (à vérifier) par contre qu'il s'agisse des géodésiques de la région II qui vont de la sphère de Schwarzschild à la singularité : des droites d'équation avec |a|>1 (peut-être même |a|=1, pour la géodésique nulle qui suit l'horizon, peut être même |a|<1, pour des géodésiques de genre espace des régions I et III, celles de t de Schwarzschild constant, dans tous les cas r_s est un extremum de r le long de la géodésique) dans un kruskal.

m@ch3

[Zefram Cochrane]

Attention, pour le photon, c'est (la masse est nulle, E/m diverge). Le cas n'existe pas en genre temps dans la région I.
m@ch3

merci pour la correction.
Il me semble que nous ayons bouclés la chute radiale de genre temps pour la région I.
Qu'elle est la meilleure suite à donner selon toi?
- continuer la chute radiale en région II (coordonnées KS) ?
- passer en chute radiale supraluminique en région I ?
_ généraliser les vitesses subluminique en région I ( vitesse de satellisation) ?
je ne serais pas étonné que de manière générale :

[mach3]

Pour moi il faut en terminer avec les géodésiques radiales d'abord, il reste très peu à faire, et il n'est pas nécessaire de travailler avec les coordonnées de Kruskal (sauf pour en faire une représentation plus "jolie") concernant la région II, il faut juste faire attention au sens des choses (t n'est pas temporel, r n'est pas un rayon, dr/dt n'est pas une vitesse coordonnée radiale...).
Pour le genre espace (ce que tu appelles supraluminique), il faudra faire attention car sera négatif, ce qui nécessitera quelques aménagement dans les formules. Peut-être remplacer par un "machin" (qu'on pourra noter K) qui s'interprète comme E²/m² seulement quand il est positif.

m@ch3

[Zefram Cochrane]

J'ai faits quelques calculs en prenant 2M = 1 et en me basant sur cette formule


pour r<2M
Voo = ALEA.ENTRE.BORNES(0;100)/100
Eo² = 1/(1-Voo^2)
Yu² = 1/(1-ALEA.ENTRE.BORNES(0;100))
Yw² =1/(1-100/ALEA.ENTRE.BORNES(1;100))
Vr = RACINE(1-Yu²/Eo²/Yw²)
E² = Eo²*Yw²/Yu²
V = RACINE(1-1/E²)
VERIF Vr - V = 0.00000000
Ce que cela nous dit c'est que lorsqu'un chuteur franchit 2M son énergie passe de +oo à -oo.
sa vitesse devient supraluminique mais E² s'accroit et devient -1 quand V = RACINE(2)
lorsque r ->2M , V devient oo et E² -> -0

[mach3]

Ce que cela nous dit c'est que lorsqu'un chuteur franchit 2M son énergie passe de +oo à -oo.

Ce n'est pas mon avis. E est une constante du mouvement, elle ne doit pas changer quand l'horizon est franchi. Par contre les rôles de t et r étant changé quand on passe l'horizon, les équations doivent être manipulées avec des pincettes pour rester valides en region II. L'expression de dr/dt doit rester correcte a priori, sauf que dr/dt ne désigne plus la même chose... A vérifier formellement quand j'aurais le temps.

m@ch3

[Zefram Cochrane]

Bonsoir, tu as raison c'est E² qui change de signe.
Toujours à partir de cette formule.


J'ai calculé l'évolution de la vitesse entre 10Rs et 0Rs pour des vitesses de départ différentes : 0 ; Vlib ; 2*Vlib; 3*Vlib.

Ce que montre le schéma est que plus la vitesse de départ est proche de c, plus la courbe colle avec celle constante de la lumière qui reste invariante au dessus et en dessous de l'horizon.
Bon j'ai tenté aussi des calculs avec des vitesses de départ supraluminique mais je n'ai rien obtenu de convainquant.
Comme tu le dis, les résultats sont à prendre avec des pincettes ; ce schéma et les calculs précédents ne sont que des esquisses qu'il convient de regarder avec la plus grande prudence.
Cordialement,
Zefram

[Mailou75]

Salut,

Ah ben si, E (et E/m) a un sens physique en connexion avec l'énergie mécanique classique.

Je veux bien mais c’est quoi pour toi E et m ?

Dans le cas de Minkowski, une géodésique, quelque soit son genre, est d'équation avec et des constantes. La distinction entre genre espace, nul ou temps n'est pas au niveau de l'expression de la géodésique, mais au niveau du genre du 4-vecteur tangent u que cela engendre, qui aura comme composantes et donc comme carré scalaire :

On voit tout suite que le genre nul correspond à et qu'on est en genre temps pour une valeur strictement inférieure en valeur absolue à 1 et de genre espace pour une valeur strictement supérieure. Avec une seule expression, on passe continument par tous les genres en faisant varier

Pas étonnant que l'équation décrivant une géodésique radiale de Schwarzschild ne présente pas de distinction a priori en fonction du genre de la géodésique... C'est le genre du 4-vecteur tangent qui fera la distinction :

Le genre nul correspond à

Ok merci, c’est très clair. (La valeur de dr/dt traduisant l’effet Shapiro)
C’est le sens de «géodésique» qui m’échappait. Je croyais qu’une géodésique était toujours de genre temps ou lumière, à cause de la définition qui en est donnée en géneral. Zef n’a pas tort quand il parle de supraluminique pour le genre espace dans ce cas !

........

J'ai calculé l'évolution de la vitesse entre 10Rs et 0Rs pour des vitesses de départ différentes

J’aurais pensé que la **vitesse** entre Rs et r=0 diminuait pour finir quasi nulle, ou du moins faible. (Si on prend en compte que t est de l’espace et qu’on fait pivoter la région II, voir représentations d’Amanuensis).

Bonne continuation