travail du champ de gravitation en relativité générale.

[yves95210]

Non, c’est bien une géodésique entrante discontinue. Voir par exemple ici https://physics.stackexchange.com/qu...al-coordinates un graph extrait du MTW. Pour ne rien te cacher c’est précisément celui ci qui m’avait permis, il y a quelque temps maintenant, de faire le lien entre Schw et Kruskal.

Alors là, tu m'en bouches un coin. Mais comme je ne me suis jamais trop intéressé à ce qui se passe à l'intérieur d'un TN (surtout vu par un observateur à l'infini), je ne suis pas une référence en la matière.
Mais si tu as raison (et ta référence au MTW te donne effectivement raison), ça voudrait dire que, même si un observateur à l'infini ne voit (photons) jamais l'objet ne traverse jamais l'horizon, il "voit" (gravitation) la masse du TN s'accroître au bout d'un temps fini. Argument que je n'avais jamais lu dans les discussions sur les TN...

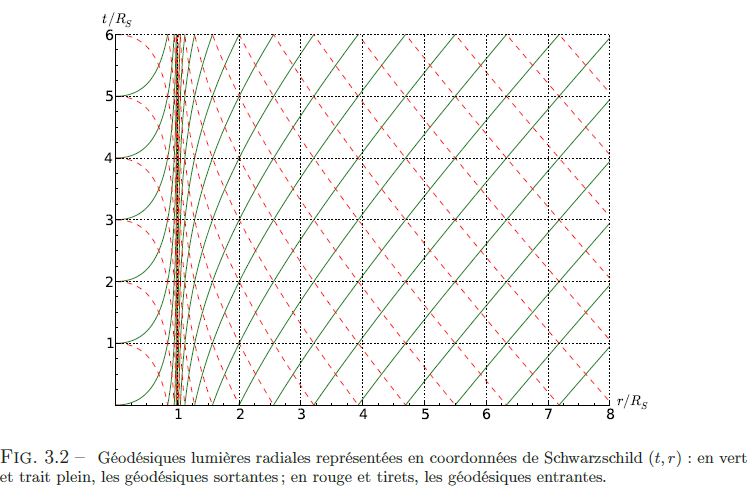
Ce qui m'ennuie, c'est que ça ne correspond pas au schéma représentant les géodésiques lumière radiales dans mon livre de cours (le Gourgoulhon).

D'accord, il ne s'agit que des géodésiques lumière, mais je suppose qu'à la limite (m -> 0) les géodésiques suivies par une particule de masse m doivent s'en rapprocher. Je reconnais que je n'y ai pas réfléchi, et qu'en matière de RG et surtout de TN il vaut mieux ne pas faire confiance à son intuition, mais quand-même...
Faudra que je jette un coup d’œil au MTW qui en dit certainement plus que le petit extrait sur ton lien stackexchange.

C’est juste. C’est une convention que je prends, je parle de vitesse positive pour la chute. Mais si tu veux être rigoureux mathématiquement il faut en effet mettre des - partout et faire un mirroir des courbes de vitesse. Il est même possible que certaines des formules citées donnent un resultat négatif, je n’y prette pas attention, ça ne change rien a l’ensemble.

OK. Pour être pointilleux, dans ce cas il faudrait que tu ajoutes un petit "-" devant les étiquettes des axes verticaux de tes diagrammes dr/dt(r).
-----

[yves95210]

PS : j'ai vérifié dans le MTW, c'est bien ça.
Et aussi pour les géodésiques lumière (figure 31.1), contrairement au schéma de Gourgoulhon, ce qui me chagrine un peu

Et je pense que ça vaut la peine de lire la page référencée à la fin du message stackexchange que tu as cité.

[Mailou75]

Re,

Mais si tu as raison (et ta référence au MTW te donne effectivement raison), ça voudrait dire que, même si un observateur à l'infini ne voit (photons) jamais l'objet ne traverse jamais l'horizon, il "voit" (gravitation) la masse du TN s'accroître au bout d'un temps fini.

Je n’ai jamais traité un tel cas, mais j’ai un doute. Pour un observateur, ce qu’il voit et ce qu’il mesure/ressent doivent rester cohérent. Je ne saurais pas te dire...

Ce qui m'ennuie, c'est que ça ne correspond pas au schéma représentant les géodésiques lumière radiales dans mon livre de cours (le Gourgoulhon).

Eric Gourgoulon c’est pourtant pas une bille, je suis perplexe. L’intérieur d’un repère de Schw doit en fait subir une rotation à 90° pour placer la cordonnée r, devenue du temps, verticalement. Amanuensis a toujours insisté sur ce point. La question est donc : arrive t on de la droite ou de la gauche ?

Toutefois, si tu regardes ceci https://forums.futura-sciences.com/a...ml#post6322504 où j’ai bêtement transposé une courbe ascension/chute vers un Kruskal, on se rend compte que le tronçon jaune, pour pouvoir restituer une continuité complète de la trajectoire, doit en réalité appartenir à la région III.

Tu le poses des colles là...

OK. Pour être pointilleux, dans ce cas il faudrait que tu ajoutes un petit "-" devant les étiquettes des axes verticaux de tes diagrammes dr/dt(r).

Je fais de la physique avant de faire des maths (mais tu as raison sur le fond). Je trace des courbes pour essayer de «sentir» les choses, et les vitesses me parlent plus en positif. D’ailleurs, toi même, en sautant depuis un arbre dirais tu que ta vitesse est négative ?

Et je pense que ça vaut la peine de lire la page référencée à la fin du message stackexchange que tu as cité.

Ouep, faudra que je prenne le temps de le lire. Je ne suis pas une flèche en anglais.

[mach3]

Il faut bien toujours se souvenir que représenter les régions I et II accolées le long de r=rs dans un repère (t,r) s'appuie implicitement sur des conventions. Ce sont deux cartes différentes. Le fait que la métrique ait la même expression dans les deux régions quand on utilise les coordonnées de Schwarzschild n'est qu'une contingence. Evidemment quand on a choisi un "sens" pour r et t, il faut s'y tenir, et selon comment on l'a choisi, la région II pourra avoir la tête en-bas ou non.

Dans la représentation de KrSz (coordonnées T,X), les iso-t sont des demi-droites radiales T=aX, la valeur de t changeant au fur et à mesure qu'on "tourne" autour du centre (la sphère de Schwarzschild T=0,X=0). On fait naturellement croitre t de -inf à +inf dans la région I, des demi-droites radiales T=-X à T=X avec X>0. Par contre il n'y a aucune façon naturelle de choisir comment varie t dans les 3 autres régions. Et comme la métrique est invariante suivant t, elle est de fait invariante quand on transforme t en -t, et bien ça ne change rien de choisir l'un ou l'autre (sauf des signes dans les formules allant de Schwarzschild à KrSz en fonction des régions)

Un choix courant (dans le MTW notamment), c'est décroissance de t=+inf en T=X (T>0) à t=-inf en T=-X (T>0) dans la région II, puis croissance de t=-inf en T=-X (X<0) à t=+inf en T=X (X<0) dans la région III et enfin décroissance de t=+inf en T=X (T<0) à t=-inf en T=-X (T<0) dans la région IV. Avec un tel choix, les entrantes en provenance de I viennent d'en haut à droite dans la région II et les entrantes en provenance de III viennent d'en bas à droite.

A noter qu'il n'y a pas de sortante dans la région II, mais que dans cette représentation, région II et région IV se superposent (tout comme I et III d'ailleurs) et les sortantes appartiennent à la région IV et sortent soit vers I soit III suivant qu'elles vont en haut à droite ou en bas à droite (ou inversement, ça dépend comment on oriente t dans la région IV...).

Les représentations avec I/II accolées le long de r=rs sont pleines de pièges si on n'a pas conscience de tout cela.

m@ch3

[yves95210]

EDIT : j'ai été très long à rédiger ce message et n'avais pas vu que mach3 avait répondu entre temps. Je n'ai pas encore lu son message, donc le mien ci-dessous n'y répond pas.

Je n’ai jamais traité un tel cas, mais j’ai un doute. Pour un observateur, ce qu’il voit et ce qu’il mesure/ressent doivent rester cohérent. Je ne saurais pas te dire...

C'est pourtant bien ce que montre le diagramme du MTW (et le tien !).

Eric Gourgoulon c’est pourtant pas une bille, je suis perplexe. L’intérieur d’un repère de Schw doit en fait subir une rotation à 90° pour placer la cordonnée r, devenue du temps, verticalement. Amanuensis a toujours insisté sur ce point. La question est donc : arrive t on de la droite ou de la gauche ?

Juste en-dessous dans le texte, pour une géodésique lumière entrante et r<Rs, Gourgoulhon donne l'équation suivante (plus simple que pour une géodésique de genre temps !)

En dérivant par rapport à r, ça donne

ce qui correspond bien aux courbes de son diagramme. J'avais pensé à une coquille dans le diagramme, mais là, s'il y a une erreur, c'est dans les équations. Et Gourgoulhon ne parle nulle part de faire subir au repère une rotation de 90° pour r<Rs (i.e. lorsque les signes des composantes en r et en t de la métrique s'inversent).
En fait son formalisme conduit à faire entrer les photons dans la région sous l'horizon à . Et même si les calculs sont plus compliqués, le résultat doit être analogue pour des particules matérielle. Cela revient à dire que tout ce qui se trouve sous l'horizon d'un TN de Schwarzschild doit s'y trouver depuis l'éternité.
C'est bien pour ça qu'on dit que la solution de Schwarzschild représente un TN éternel, autrement dit existant depuis la naissance de l'univers (bref c'est une solution mathématique, mais pas trop physique...).

Mais si la bonne description physique est plutôt celle que donnent MTW, elle reviendrait bien à dire que dans le temps propre d'un observateur distant, l'objet qui n'atteint l'horizon qu'au bout d'une durée infinie "remonte le temps"^(*) depuis jusqu'à l'instant où il atteint la singularité centrale. Ce qui conduit bien à un accroissement de la masse du TN (et donc du rayon de son horizon) en un temps fini pour l'observateur. Et selon la flèche du temps de cet observateur, à partir de cet instant et pour toujours, la masse du TN inclut celle de l'objet.
(*) ça ne me choque pas plus que ça, dans la mesure où ça concerne une région de l'espace-temps causalement séparée de la nôtre.

Il faudrait juste que je comprenne par quel tour de passe-passe MTW arrivent à cette représentation à partir des équations... Mais je pense que c'est dans un autre chapitre. Et il faut aussi que je lise la page citée plus haut. Si j'y vois plus clair après ça je reviendrai t'en parler...

[Mailou75]

Merci

Par contre il n'y a aucune façon naturelle de choisir comment varie t dans les 3 autres régions. Et comme la métrique est invariante suivant t, elle est de fait invariante quand on transforme t en -t, et bien ça ne change rien de choisir l'un ou l'autre (sauf des signes dans les formules allant de Schwarzschild à KrSz en fonction des régions)

Bon ben voilà, les deux sont justes, juste un choix de convention. S’aurait été étonnant de la part de Gourgoulhon...

[Mailou75]

Re,

C'est pourtant bien ce que montre le diagramme du MTW (et le tien !)

Non du tout, le rayon du trou noir ne change pas. Je n’ai jamais traité ce cas, trop compliqué...

Cela revient à dire que tout ce qui se trouve sous l'horizon d'un TN de Schwarzschild doit s'y trouver depuis l'éternité.

Ce serait plutôt l’inverse. Tous les évènement contenus dans un trou blanc (IV) sont dans le passé de l’extérieur (I). Tous les évènements contenus dans un trou noir (II) sont dans le futur de l’extérieur (I). Si on ressent une gravité en région I, elle provient du trou blanc, pas du trou noir. Quand on met le nez dedans, on voit que la vulgarisation «élude certains détails»...

Ce qui conduit bien à un accroissement de la masse du TN (et donc du rayon de son horizon) en un temps fini pour l'observateur. Et selon la flèche du temps de cet observateur, à partir de cet instant et pour toujours, la masse du TN inclut celle de l'objet.

Les objets qu’on fait tomber dedans sont des particules test de masse négligeable. On néglige leur masse et donc la variation de Rs potentielle. Sinon on tombe dans le problème à deux corps, très compliqué... Mais sinon je suis plutôt d’accord avec toi sur le fond : si un objet appartient au système alors sa masse doit déjà être comprise pour définir Rs. C’est pour ça que j’ai du mal avec les diagrammes d'effondrement où l’horizon «apparait» a un moment donné. Oppenheimer ne raconte sans doute pas n’importe quoi, mais comme dit je n’ai jamais traité ce sujet. Plutot que raconter n’importe quoi il faudra que je m’y attelle...

[mach3]

Mais si la bonne description physique est plutôt celle que donnent MTW, elle reviendrait bien à dire que dans le temps propre d'un observateur distant, l'objet qui n'atteint l'horizon qu'au bout d'une durée infinie "remonte le temps"^(*) depuis jusqu'à l'instant où il atteint la singularité centrale.
(*) ça ne me choque pas plus que ça, dans la mesure où ça concerne une région de l'espace-temps causalement séparée de la nôtre.

attention, t n'est pas une coordonnée temporelle pour r<rs, c'est une coordonnée spatiale, donc il n'y a pas de "remontée dans le temps". Les cônes de lumière sont "couchés" dans la région II, les lignes d'univers entrantes vont de r->rs à r=0 en allant du passé vers le futur (et c'est l'inverse dans la région IV pour les sortantes). Selon si elles viennent de t=+inf ou -inf, elles arrivent des régions I ou III. si elles viennent de t fini, alors elles proviennent directement de la région IV via la sphère de Schwarzschild (en particulier, les horizontales t=cst en région II (r<rs) sont des géodésiques de genre temps provenant directement de la région IV, à contraster avec les horizontales t=cst en région I (r>rs) qui sont des géodésiques de genre espace).

m@ch3

[yves95210]

Non du tout, le rayon du trou noir ne change pas. Je n’ai jamais traité ce cas, trop compliqué...

Et pourtant si, elle change, même si c'est de manière infinitésimale - ce que tu peux bien sûr négliger dans les calculs lorsque tu étudies la trajectoire d'une particule test de masse négligeable. Mais en fait c'est ce que tu dis ci-dessous.

Les objets qu’on fait tomber dedans sont des particules test de masse négligeable. On néglige leur masse et donc la variation de Rs potentielle. Sinon on tombe dans le problème à deux corps, très compliqué... Mais sinon je suis plutôt d’accord avec toi sur le fond : si un objet appartient au système alors sa masse doit déjà être comprise pour définir Rs. C’est pour ça que j’ai du mal avec les diagrammes d'effondrement où l’horizon «apparait» a un moment donné. Oppenheimer ne raconte sans doute pas n’importe quoi, mais comme dit je n’ai jamais traité ce sujet. Plutot que raconter n’importe quoi il faudra que je m’y attelle...

J'ai lu la page dont je te parlais (en fait un chapitre d'un bouquin), ça éclaircit pas mal les choses, en tout cas à mon goût. Je t'encourage à en faire autant si ton allergie à l'anglais n'est pas trop forte. Et sinon, un coup de google trad. Tiens je t'en colle un extrait ici, traduit par google et à peine corrigé, histoire de t'allécher, puisque ça dit que la suite va répondre à la question que tu te poses ci-dessus :

(...) deux faits apparemment contradictoires:

(1) Un horizon des événements ne peut croître que si la masse contenue à l'intérieur de cet horizon augmente.

(2) Rien ne traverse l'horizon des événements dans un temps fini en coordonnées de Schwarzschild.

Le point (1) est une conséquence du fait que, comme dans le cas de la gravité newtonienne, le champ créé par une coque sphérique (statique) à l'intérieur est nul; il est donc impossible d'élargir l'horizon des événements en accumulant de la masse à l'extérieur. Néanmoins, si la masse s'accumule près de l'extérieur de l'horizon des événements d'un trou noir, le rayon de gravité du système combiné doit finalement augmenter suffisamment pour englober la masse accumulée, ce qui conduit inévitablement à la conclusion que la matière de l'extérieur doit atteindre l'intérieur et doit le faire de manière perceptible pour un observateur distant en un temps fini, ce qui semble directement en contradiction avec le point 2 (et semble certainement incompatible avec l’interprétation de "l’étoile figée"). Pour résoudre ce paradoxe apparent, il est nécessaire d’examiner avec soin la définition du trou noir et le comportement de la coordonnée temporelle de Schwarzschild près de l'horizon.

PS : @ mach3, encore une fois, je n'ai vu ton nouveau message qu'après avoir fini de rédiger celui-ci. J'y répondrai peut-être plus tard. Mais peux-tu jeter un coup d’œil au document évoqué ci-dessus (https://www.mathpages.com/rr/s7-02/7-02.htm) et nous dire si tu trouves que ça tient la route ?

[yves95210]

attention, t n'est pas une coordonnée temporelle pour r<rs, c'est une coordonnée spatiale, donc il n'y a pas de "remontée dans le temps". Les cônes de lumière sont "couchés" dans la région II, les lignes d'univers entrantes vont de r->rs à r=0 en allant du passé vers le futur (et c'est l'inverse dans la région IV pour les sortantes).

Oui, ça je l'ai compris. Au moins avec les équations, parce que sinon j'ai du mal à me représenter la chose.
Et il n'y a évidemment pas de remontée dans le temps du point de vue de l'objet qui chute vers la singularité (et donc dans son temps propre τ).

Mais alors, explique-moi de quoi parlent MTW dans leur figure 31.1, où ils tracent la géodésique radiale de genre temps suivie par une particule test, qui atteint la singularité r=0 en un temps fini en coordonnées de Schw. après avoir traversé l'horizon à t =+infini, et dont la légende dit explicitement que t décroit ensuite alors que τ continue de croître.
Certes un observateur à l'intérieur de l'horizon (le pauvre...) qui utiliserait les coordonnées de Schw. ressentirait un déplacement suivant l'axe r comme un déplacement temporel et un déplacement suivant l'axe t comme un déplacement spatial, ce qui évite le paradoxe temporel.
Mais qu'est-ce que ça change pour l'observateur à l'infini, dont t est le temps propre, et qui, à défaut de voir un objet traverser l'horizon, serait capable de mesurer l'augmentation de la masse du trou noir - si du moins la figure du MTW a un sens - là encore sans qu'il y ait de paradoxe temporel, puisque, dans le futur de l'instant où il constate son augmentation et jusqu'à t infini (si rien d'autre ne tombe dans le trou noir) cette masse restera constante.

Idem dans la figure 31.5, avec à gauche le même diagramme en coord de Schw. que dans la figure 31.1, et à droite en coord de Kruskal, où la même géodésique part de la région I et traverse la région II pour atteindre r=0. Avec comme commentaire le fait que cette géodésique paraît bien plus raisonnable en coord de Kruskal - puisqu'il n'y a plus le problème (apparent) de causalité dû à la représentation de Schw.

[mach3]

En 31.1, ils représentent simplement des geodesiques en coordonnées de Schwarzschild avec les régions I et II accolées le long de la droite r=rs (qui n'appartient pas à l'espace-temps).

Le fait que les deux régions soient accolées, et que les mêmes coordonnées r et t y soient utilisées est trompeur. Il s'agit de deux ouverts disjoints de l'espace-temps de Schwarzschild. A part le fait qu'ils partagent les mêmes noms de coordonnées, il n'y a aucune raison physique de les représenter accolés.

r et t des sont champs scalaires de l'espace-temps de Schwarzschild avant d'être des coordonnées (ce qu'ils ne sont pas partout d'ailleurs, en r=r_s justement), tels que les 1-formes dt et dr soient orthogonales (pas de terme en drdt dans l'expression de la métrique) et que l'ensemble des événements de même r et t forment une sphère de surface 4\pi r^2 (en fait deux...). Les genres de dr et dt ne sont pas fixes sur tout l'espace-temps.

Il se trouve que pour r grand, r ressemble à une coordonnée radiale classique et t ressemble à une coordonnée temporelle classique, mais c'est juste une ressemblance. t n'est le temps de l'observateur immobile à l'infini qu'à l'infini. Et il n'est pas le seul champ scalaire à posséder cette propriété, par exemple la coordonnée temporelle t_r de Gullstrand-Painlevė fait la même chose (et elle au moins elle reste temporelle partout...) : il n'y a pas de façon univoque de mettre en place une datation qui coïncide avec le temps propre de l'immobile à l'infini.

Faire cette datation avec t de Schwarzschild limite forcément à la region r>r_s car dt n'est pas de genre temps pour r<r_s. Elle n'a aucun sens à l'intérieur. Une datation avec r est possible, mais n'a aucun sens pour l'immobile à l'infini : il s'agit pour lui de dates ultérieure à l'infini futur (ou antérieures à l'infini passé).
Une datation avec t_r de Gullstrand-Painlevė s'étend par contre à l'intérieur sans souci (soit en region IV, soit en II, mais pas les deux en même temps par contre).

Je m'arrête ici pour ce soir.

m@ch3

[yves95210]

Salut,

juste pour corriger mon dernier message: la deuxième figure du MTW dont je parle est la 31.4 et non la 31.5 (mais c'est dans la section 31.5).

Pour le reste, mach3, je suis d'accord avec ce que tu dis,

Faire cette datation avec t de Schwarzschild limite forcément à la region r>r_s car dt n'est pas de genre temps pour r<r_s. Elle n'a aucun sens à l'intérieur. Une datation avec r est possible, mais n'a aucun sens pour l'immobile à l'infini : il s'agit pour lui de dates ultérieure à l'infini futur (ou antérieures à l'infini passé).

mais les figures du MTW m'ont perturbé...
Et je n'ai toujours pas compris ce qu'elles représentent. Pour moi, dt/dr < 0 pour une géodésique radiale entrante, y compris pour r<Rs, alors que MTW représentent cette géodésique par une courbe de pente positive dans la région II. Si c'est juste une convention avec inversion du signe de t dans cette région histoire de pouvoir représenter cette géodésique sur le même diagramme que pour la région I, ils pourraient le dire, non ? Et ils n'auraient pas écrit que t décroit alors que τ continue de croître ?

[Mailou75]

Salut Yves,

J'ai lu le doc sur la croissance des trou noir. Très interessant effectivement, je ne dirais pas que j'ai tout compris…
Je vais essayer de répondre à certaines de tes interrogations, c'est un peu en vrac car ce n'est pas encore bien rangé dans ma tête

- Concernant la décroissance de t qui t'embête à l'intérieur : Je dirais qu'elle va servir à ce que tous les autres systèmes que Schw (Kruskal, Penrose, Eddington-Finkelstein, Painlevé, Lemaitre etc...) puissent avoir des trajectoires continues entre intérieur et extérieur. Si on ne fait pas ce choix, alors aucun système ne fonctionnera.

- Pour la figure 31.4 du MTW (qui contient la 31.1) : Je ne sais pas pour les trajectoires C et D mais les A, B, E sont "schématiquement" justes. Par contre la F est fausse, elle devrait être incurvée dans l'autre sens comme le montre le Kruskal à droite ici https://forums.futura-sciences.com/a...ml#post6342819.

- Le fait qu'il n'y ait pas de "problème apparent de causalité" en Kruskal est pour moi une arnaque (de même qu'en Penrose) puisque le point sur l'horizon n'est pas défini mathématiquement (Les région I et II y sont donc dissociées autant qu'en Schw). Par contre il l'est en coordonnées de Painlevé, d'Eddington-Finkelstein ou Lemaitre. Dans le doc, le point essentiel évitant les problème de causalité semble être simplement qu'il n'existe pas de géodésique de genre temps qui puisse aller plus vite que la lumière (ce qui semble être un évidence).

- Topologie du "pantalon" : Je suis tout à fait d'accord avec cette version puisque la largeur d'une jambe est le diamètre du trou noir (~sa masse) et qu'en additionnant les deux diamètres on obtient une nouvelle jambe (~somme des masse). C'est comme dire que deux trous noirs qui se touchent forment un seul trou noir les englobant tous les deux. Je suis partisan de cette image même si on ne trouvera jamais de tels cas dans la réalité...

- Le deuxième schéma du doc est ce que perso j'ai appelé le système de coordonnées Newton + (même lien https://forums.futura-sciences.com/a...ml#post6342819). Et le troisième s'apparente plutôt à la représentation d'un effondrement en coordonnées d'Eddington-Finkelstein du genre http://www.planetastronomy.com/speci...ov/TN-cos7.jpg mais j'avoue que le passage du deuxième au troisième me fait un peu mal au crane...

- Ils m'ont un peu égaré quant ils disent que l'horizon est devant dans le temps comme "minuit est à l'infini spatial devant". Une formulation étrange mais qui revient tout de même au fait que le trou noir appartient à l'infini futur de l'extérieur, ce que montre assez bien leur dernière figure : aucune tranche d'espace de t constant ne pénètre le trou noir. Je dirais qu'il manque au doc un dernier schéma montrant une stalactite qui va s'élargir pour chaque nouvelle particule entrante.

- J'aime assez leur idée de "principe d'exclusion" lié à une courbe de densité (qu'on aurait bien aimé voir) visant à ce qu'une certaine quantité de masse ne puisse être contenue que dans un volume limité, un genre de successions d'horizons déjà établi. Une nouvelle règle régissant l'univers, pourquoi pas, mais qui pourrait poser des problème de "centre" (autour de quel point ces sphère sont elles centrées ?)

Bon, je ne sais pas si je t'aurais beaucoup aidé… en tout cas le doc est un peu plus éclairant que les diagrammes d'effondrement en coordonnées de Penrose qui m'ont toujours semblé ineptes. Merci d'avoir insisté pour nous le faire lire

A bientôt

Mailou

[mach3]

@ yves

Le MTW a beau peser 3kg, il est loin d'être exhaustif (ce qui est quelque peu effrayant...). A titre d'exemple, ils ne discutent que d'un petit nombre de système de coordonnées de la géométrie de Schwarzschild, et parfois de façon plutôt succincte.
Je n'ai pas lu l'intégralité du chapitre concerné, mais je suis pas étonné qu'ils ne précisent pas. Les sens qu'ils ont choisi pour t dans les différentes régions leurs paraissaient peut-être évidents pour différentes raisons (notamment peut-être des formules de changement de coordonnées plus simples ou élégantes).

Personnellement, les sens qu'ils ont choisi me semblent appropriés (je pourrais détailler les raisons, qui n'ont rien de physique), mais je ne suis pas choqué qu'on en inverse certains.

Je vais revenir sur la suite du message d'hier plus tard.

m@ch3

[yves95210]

Salut Mailou,

et merci pour ta réponse.

- Pour la figure 31.4 du MTW (qui contient la 31.1) : Je ne sais pas pour les trajectoires C et D mais les A, B, E sont "schématiquement" justes. Par contre la F est fausse, elle devrait être incurvée dans l'autre sens comme le montre le Kruskal à droite ici https://forums.futura-sciences.com/a...ml#post6342819.

Là je ne te suis pas : si les courbes A (géodésique entrante de genre temps partant de l'infini) et B (géodésique lumière entrante) sont correctes, je ne vois pas pourquoi la F (géodésique entrante de genre temps d'une particule partant au repos de r=5,2 Rs) serait fausse, au moins dans sa forme générale. D'ailleurs elle ressemble à ta courbe verte...

Quant au document sur la croissance des trous noirs, à propos du même cas il dit

We saw that the radial position of a test particle starting at radius r = 10m and t = 0 (for example) as a function of the particle’s proper time is a simple cycloid right down to r = 0, whereas if the same trajectory is described in terms of Schwarzschild coordinate time, the infalling object traverses through infinite coordinate time in order to reach the event horizon, and then traverses back through an infinite range of coordinate times until reaching r = 0 (in the interior) in a net coordinate time that is not too different from the elapsed proper time. In other words, the object goes infinitely far into the "future" (of coordinate time), and then infinitely far back to the "present" (also in coordinate time), and since these two segments must always occur together, we can "re-normalize" the round trip and just deal with the net change in coordinate time (for any radius other than precisely r = 2m).

et plus loin il explique pourquoi cela ne constitue pas un paradoxe temporel :

One possible objection to the physical significance of the Schwarzschild time coordinates is the fact that a single infalling object occupies two different places (one inside and one outside the event horizon) at the same coordinate time. However, this shouldn't be surprising, because worldlines need not be single-valued in terms of arbitrary curvilinear coordinates. Still, it might seem that this "dual presence" opens the door to time-travel paradoxes. For example, we can observe the increase in the gravitational radius at some finite coordinate time, when the particle that caused the increase has still not yet crossed the event horizon (using the terms "when" and "not yet" in the sense of coordinate time), so it might seem that we have the opportunity to retrieve the particle before it crosses the horizon, thus preventing the increase that triggered our retrieval! However, if we carefully examine the path of the particle, both outside and inside the event horizon, we find that by the time it has gotten "back" close to our present coordinate time on the interior branch, the exterior branch is past the point of last communication. Even a photon could not catch up with it prior to crossing the horizon. The "backward" portion of the particle's trajectory through coordinate time inside the horizon ends just short of enabling any causality paradoxes.
(...)
It’s also worth noticing that the two strategies described above for explaining the formation and growth of black holes are essentially the same. In both cases the event horizon "reaches back" to us all the way from future null infinity. In a sense, that's why the infalling geodesics in Schwarzschild space go to infinity at the event horizon.

Le dernier paragraphe doit être mis en relation avec le passage que j'avais traduit dans mon message d'hier :

if mass accumulates near the exterior of a black hole's event horizon the gravitational radius of the combined system must eventually increase far enough to encompass the accumulated mass, leading unavoidably to the conclusion that matter from the outside must reach the interior, and it must do so in a way that is perceptible in finite coordinate time for a distant observer,

Autrement dit, ce n'est que pour un TN statique idéal (i.e. situé dans un espace parfaitement vide) que l'horizon se situe à l'infini dans le futur d'un observateur à l'infini. La solution de Schwarzschild avec Rs (et donc M) constant ne s'applique qu'à cet objet mathématique. Dans l'univers réel, dès que des particules massives s'accumulent "assez près" de l'horizon, son rayon augmente en un temps fini en coordonnées de Schw, et donc pour l'observateur. L'observateur ne voit pas les particules tomber à travers l'horizon, mais plutôt l'horizon grandir pour avaler ces particules. Et plus l'horizon du TN grandit, plus il se rapproche temporellement de l'observateur.

Je ne sais pas ce que vaut cette explication, que je n'avais pas lue ailleurs, mais elle me plaît bien...

NB: ce document en ligne est en fait un chapitre d'un livre : en revenant à la table des matières via le lien en bas de la page, on y trouve des liens vers plusieurs sites de vente en ligne proposant la version papier, entre autres Amazon.
L'auteur (anonyme sur le site internet mathpages) est un certain Kevin Brown, parfaitement inconnu selon un commentaire d'un lecteur, qui soupçonne qu'il s'agit d'un pseudonyme. En cherchant "Kevin Brown physics" sur google, je suis tombé entre autres sur des discussions sur physicsforum, où la question de son identité est posée - ça a l'air d'être un mystère...
Raison pour laquelle j'aimerais bien que quelqu'un de plus compétent que moi nous donne son avis sur ce document.

[Mailou75]

Salut,

Là je ne te suis pas : si les courbes A (géodésique entrante de genre temps partant de l'infini) et B (géodésique lumière entrante) sont correctes, je ne vois pas pourquoi la F (géodésique entrante de genre temps d'une particule partant au repos de r=5,2 Rs) serait fausse, au moins dans sa forme générale. D'ailleurs elle ressemble à ta courbe verte...

Juste le Kruskal est faux pardon. La trajectoire F doit être incurvée dans l’autre sens (comme toutes celles qui ont leur apoastre en t=0, pour ça que je te donnais mon lien graphique).

Dans l'univers réel, dès que des particules massives s'accumulent "assez près" de l'horizon, son rayon augmente en un temps fini en coordonnées de Schw, et donc pour l'observateur. L'observateur ne voit pas les particules tomber à travers l'horizon, mais plutôt l'horizon grandir pour avaler ces particules.

Ils disent aussi que dès qu’on prend en compte une masse non négligeable, on tombe dans un problème à deux corps (une grosse et une toute petite jambe si tu veux). Ca correspondrait à la figure de droite ici https://forums.futura-sciences.com/a...ml#post6186129, le gros «avale» le petit mais en fait les deux fusionnent : le diamètre final est la somme des diamètres (somme des masses), comme le pantalon. On a un nouveau trou noir, le déplacement du centre + changement de diamètre engendre une mise a jour du champ, cad des ondes gravitationnelles (pour le toy bien sur... en vrai ça va valser). Le passage théorique est instantané, je ne sais si une étude plus poussée révèlerait autre chose que «changer de rayon», à notre niveau j’entends...

Et plus l'horizon du TN grandit, plus il se rapproche temporellement de l'observateur.

J’ai un peu de mal avec cette notion de temps-distance. C’est flou, même dans le texte.

Raison pour laquelle j'aimerais bien que quelqu'un de plus compétent que moi nous donne son avis sur ce document.

Que moi aussi, tu peux le dire clairement je ne me vexerais pas, je connais mes limites

[mach3]

Vous postez bien trop de choses par rapport à mes disponibilités de ce week-end tous les deux, j'ai du mal à suivre et pourtant certaines erreurs doivent être corrigées.

De plus, ne serait-ce pas mieux de scinder la discussion?

Concernant les trous noirs en croissance, il n'est pas très malin de raisonner avec la géométrie de Schwarzschild qui est par nature statique et donc sans croissance. Il faut aller un peu plus loin et considérer des géométries et peu plus compliquées.
Cas le plus simple, considérer de fines coquilles (de préférence faites de rayonnement, c'est plus facile à
traiter) concentriques (on conserve ainsi la symétrie sphérique) en chute libre, avec du vide entre chaque. On aura un patchwork de géométries de Schwarzschild de différents paramètres M, accolées le long des coquilles.
Un peu plus complexe (pas encore abordé personnellement), il y a la géométrie de Vaidya. Toujours en symétrie sphérique, mais remplie de rayonnement entrant ou sortant.
Si on veut aller plus loin, on sort de la symétrie sphérique et c'est hard...
Si on veut rester sans rotation, il faut considérer des chutes radiales uniquement. Dans le vide au loin, ça tend toujours vers Schwarzschild (ou kerr si pas radial), et les ondes gravitationnelles émises par le couple trou noir - objet en chute mettent à jour le champ au loin pour prendre en compte l'accroissement de la masse. Les OGs vont se comporter comme les EM : émises de plus en plus près du trou noir, elles sont de plus en plus redshiftée vu de loin. L'observateur lointain reçoit la quasi-totalité de l'information électromagnétique et gravitationnelle en une durée finie relativement courte (la totalité en une durée infinie si ce n'est pas quantifié), et donc la géométrie lointaine tend en fait très vite vers celle d'un trou noir de masse accrue par la masse en chute, moins la masse "perdue" par émissions d'ondes.
Bon tout ça c'est ce que j'ai compris "avec les mains"...

Ce sera tout pour ce matin je pense. En attendant mailou, essaie de ne pas dire trop de bêtises, comme par exemple ce qui suit et sur lequel on reviendra quand j'aurais le temps :

- Le fait qu'il n'y ait pas de "problème apparent de causalité" en Kruskal est pour moi une arnaque (de même qu'en Penrose) puisque le point sur l'horizon n'est pas défini mathématiquement (Les région I et II y sont donc dissociées autant qu'en Schw). Par contre il l'est en coordonnées de Painlevé, d'Eddington-Finkelstein ou Lemaitre. Dans le doc, le point essentiel évitant les problème de causalité semble être simplement qu'il n'existe pas de géodésique de genre temps qui puisse aller plus vite que la lumière (ce qui semble être un évidence).*

m@ch3

[Mailou75]

Salut,

Ce sera tout pour ce matin je pense. En attendant mailou, essaie de ne pas dire trop de bêtises, comme par exemple ce qui suit et sur lequel on reviendra quand j'aurais le temps :

Je parlais «d’arnaque» pour le raccord des trajectoires sur l’horizon chez Kruskal et Penrose. Mais les autres ne font pas mieux... chez Painlevé, Eddington-Finkelstein, Lemaitre... c’est l’espace (à t constant) qui n’est pas défini. Ce n’est qu’un changement de représentation des mêmes «coordonnées», la solution de Schwarzschild, l’info ne change pas d’un système à l’autre, «l'arnaque» est juste déplacée. Mais si ce n’est pas le cas tu me corrigera (pas trop severement)

[yves95210]

Salut,

Juste le Kruskal est faux pardon. La trajectoire F doit être incurvée dans l’autre sens (comme toutes celles qui ont leur apoastre en t=0, pour ça que je te donnais mon lien graphique).

OK

Ils disent aussi que dès qu’on prend en compte une masse non négligeable, on tombe dans un problème à deux corps (une grosse et une toute petite jambe si tu veux). Ca correspondrait à la figure de droite ici https://forums.futura-sciences.com/a...ml#post6186129, le gros «avale» le petit mais en fait les deux fusionnent : le diamètre final est la somme des diamètres (somme des masses), comme le pantalon. On a un nouveau trou noir, le déplacement du centre + changement de diamètre engendre une mise a jour du champ, cad des ondes gravitationnelles (pour le toy bien sur... en vrai ça va valser). Le passage théorique est instantané, je ne sais si une étude plus poussée révèlerait autre chose que «changer de rayon», à notre niveau j’entends...

Oui. Je ne suis pas allé voir le message que tu cites, mais ça me semble évident. J'avais utilisé le même argument dans une vieille discussion sur les TN. (en pratique, la masse du TN final est plus petite que cette somme parce qu'une partie de l'énergie est rayonnée).

Et plus l'horizon du TN grandit, plus il se rapproche temporellement de l'observateur.

J’ai un peu de mal avec cette notion de temps-distance. C’est flou, même dans le texte.

C'est assez simple à comprendre :
- Pour un "vrai" TN de Schwarzschild l'horizon des événements est initialement à l'infini dans le futur de l'observateur à l'infini.
- Quand le TN de masse initiale M et rayon R "avale" une étoile de masse ΔM (c'est-à-dire dès que, du point de vue de l'observateur, la matière de cette étoile s'est suffisamment écrabouillée au voisinage de l'horizon pour qu'elle soit entièrement contenue à l'intérieur de la sphère de rayon R+ΔR, avec ΔR=ΔM) cela a pour effet d'augmenter le rayon du TN de ΔR. Et cela se produit au bout d'un intervalle de temps fini Δt₁ pour l'observateur, puisque ça ne demande pas que cette masse ait traversé l'horizon initial de rayon R. Autrement dit, pour l'observateur le nouvel horizon est moins loin dans le temps (puisque Δt₁<+∞).
- Si une deuxième étoile de même masse subit le même destin, il suffit que, toujours du point de vue de l'observateur, la masse totale des deux étoiles soit contenue à l'intérieur de la sphère de rayon R+2ΔR, ce qui se produit au bout d'un intervalle de temps Δt₂<Δt₁. Autrement dit, l'horizon s'est encore rapproché dans le temps.

Et ainsi de suite. Sauf que l'observateur n'a plus affaire à un "vrai" TN de Schwarzschild puisque sa masse et son rayon augmentent progressivement.

Mais ce n'est qu'une raison de plus de penser que la solution de Schwarzschild n'est qu'un modèle mathématique très insuffisant pour représenter la réalité physique (idem pour Kerr, déjà plus réaliste car il est très peu probable que les TN "réels" ne soient pas en rotation; mais le même raisonnement à propos du grossissement des TN peut s'y appliquer).

Je m'étais laissé convaincre du fait qu'on ne pouvait parler de TN que "FAPP", grâce au fait que, même si leur horizon se situe à l'infini dans notre futur, au bout d'un temps fini on ne reçoit plus de rayonnement de la matière située à l'extérieur d'un TN au voisinage immédiat de son horizon (l'argument du dernier photon avant l'horizon utilisé entre autres par MTW).
Il me semble que l'explication ci-dessus prouve que l'horizon des TN qu'on observe "existe" réellement (et pas seulement FAPP) dans notre présent - et que l'approximation consistant à utiliser les solutions de Schwarzschild ou de Kerr pour représenter l'espace-temps autour d'un TN n'est valable que sur un intervalle de temps durant lequel on peut considérer que l'augmentation de sa masse est négligeable (mais cet intervalle est évidemment bien plus long que la durée de nos observations, sauf en cas de fusion d'un TN stellaire avec une étoile de masse comparable ou un autre TN; donc c'est légitime d'utiliser la solution de Kerr pour décrire l'espace-temps, par exemple autour du TN supermassif de M87).

[yves95210]

@mach3 : Il me semble qu'on s'est beaucoup éloigné du sujet initial de la discussion (le "travail du champ de gravitation en RG")... Cela vaudrait peut-être la peine de scinder ce fil, non ?
Je ne sais pas à partir d'où, car j'avais juste jeté un coup d’œil au début de la discussion, et ne suis revenu lire les nouveaux messages qu'à partir de celui où Mailou a posté ses diagrammes (j'étais curieux de voir à quoi avait abouti le fil qu'il avait ouvert dans le forum Physique). Mais ça n'avait déjà qu'un rapport assez indirect avec le sujet initial.
J'ai rarement le courage de lire les entre Mailou et Zefram, donc je ne sais pas comment la discussion a évolué d'un sujet à l'autre.
(Mailou, désolé pour le smiley, je n'en ai pas trouvé où ce sont des pages d'équations qui sont échangées entre les deux interlocuteurs...)

[yves95210]

PS :

ça n'avait déjà qu'un rapport assez indirect avec le sujet initial.

en fait si... Fallait suivre
C'est moi qui ai fait dévier la discussion à partir de mes remarques sur les courbes de Mailou. Désolé.
Ceci dit le sujet de la croissance des TN et de ses conséquences sur la vision qu'on en a (théorique et expérimentale) me semble mériter un fil à part entière.

[yves95210]

Salut mach3,

Désolé, je n'avais pas vu ton message de ce matin...

De plus, ne serait-ce pas mieux de scinder la discussion?

Oui, c'est aussi ce que je suggérais (cf. mes derniers messages, postérieurs au tien).

Je continue quand-même ici pour le moment, même si ça s'écarte de plus en plus du sujet initial.

Concernant les trous noirs en croissance, il n'est pas très malin de raisonner avec la géométrie de Schwarzschild qui est par nature statique et donc sans croissance. Il faut aller un peu plus loin et considérer des géométries et peu plus compliquées.
Cas le plus simple, considérer de fines coquilles (de préférence faites de rayonnement, c'est plus facile à traiter) concentriques (on conserve ainsi la symétrie sphérique) en chute libre, avec du vide entre chaque. On aura un patchwork de géométries de Schwarzschild de différents paramètres M, accolées le long des coquilles.
Un peu plus complexe (...)

Oui, si on veut aller plus loin que le raisonnement "avec les mains" que j'ai proposé dans le message #109, et qui ressemble en fait à ce que tu proposes ci-dessus.

Quant aux solutions "plus compliquées" (mais celle qui suit ne l'est pas trop):

Dans le cas sans rotation, j'ai aussi pensé qu'il serait possible d'utiliser la métrique LTB (à symétrie sphérique mais non homogène), en traitant le collapse d'une zone de sur-densité d'un univers "de poussière" par ailleurs (asymptotiquement) homogène.
Cela n'a rien de très original, mais je ne m'étais jamais posé la question de la formation d'un horizon des événements (en général, quand les astrophysiciens étudient le collapse d'une zone sur-dense, l'idée est plutôt que cela conduit à la formation d'une structure virialisée - car on n'est pas dans le cas idéal où toutes les particules suivent le flux comobile -, dans laquelle la métrique LTB ne s'applique plus. Bref j'avais déjà fait l'exercice, mais sans aller plus loin et sans penser à vérifier si on pouvait arriver à la formation d'un horizon).
Une petite recherche sur "event horizon LTB metric" remonte plusieurs publications (https://arxiv.org/abs/0812.5108v3, https://arxiv.org/abs/1312.2860v2, ...). Je n'ai fait que les parcourir, mais voici la conclusion de la première :

Unlike models discussed so far in the literature, we have constructed models of mass condensation within the FRW universe leading to cosmological black holes without having the usual pathologies we know from other models: the cosmic fluid is dust and ideal producing a singularity at the center in the course of time. The central singularity is spacelike and not naked. In the case of flat or open universe models the singularity is weak and has distinct apparent and event horizons. The apparent horizons are not everywhere spacelike, to be compared with the Schwarzschild one which is null everywhere. This has already been noticed in a general context by [36]. While the apparent horizon is defined by the surfaces R = 2M, similar to the Schwarzschild horizon, the event horizon is further away. Models we have proposed show that one has to expect new effects while considering dynamical cosmic black holes. The simple Schwarzschild static model may not reflect all the phenomena one may expect in observational cosmology, and the black hole thermodynamics. Even the simple concept of mass is not a trivial one in such a dynamical environment.

[Zefram Cochrane]

PS :

en fait si... Fallait suivre
C'est moi qui ai fait dévier la discussion à partir de mes remarques sur les courbes de Mailou. Désolé.
Ceci dit le sujet de la croissance des TN et de ses conséquences sur la vision qu'on en a (théorique et expérimentale) me semble mériter un fil à part entière.

Bonjour,
Je suis d'accord sur le fait que la croissance des TN méritent leur sujet à part entière, mais comme le sujet et noamment les passages de régions à une autre et ce que cela implique pour les différents observateurs m'intéresse également que vous poursuiviez sur ce fil m'arrange en fait.
J'avoue être largué sur certains points, mais je poserais des questions si nécessaire.

[yves95210]

Salut Zefram,

Bonjour,
Je suis d'accord sur le fait que la croissance des TN méritent leur sujet à part entière, mais comme le sujet et noamment les passages de régions à une autre et ce que cela implique pour les différents observateurs m'intéresse également que vous poursuiviez sur ce fil m'arrange en fait.
J'avoue être largué sur certains points, mais je poserais des questions si nécessaire.

Il vaudrait quand-même mieux séparer les deux sujets que tu évoques, l'un (la croissance des TN) ne pouvant pas être traité correctement dans le cadre du modèle de Schwarzschild, alors que l'autre est directement lié à ce modèle (univers vide à part la masse centrale et d'éventuelles particules test de masse négligeable par rapport à la masse centrale).

Le second sujet, ce que le passage d'un objet de la région I à la région II implique pour les observateurs (et en particulier pour un observateur "à l'infini"), ne peut pas être traité correctement avec Schwarzschild si ce passage conduit à une augmentation non négligeable du rayon de l'horizon. Si on s'en tient au modèle de Schwarzschild, tous les objets sont de masse négligeable, et même la somme de leurs masses est négligeable par rapport à la masse centrale... Rs n'augmente jamais, et du point de vue d'un observateur à l'infini il ne se passe rien d'autre que le résultat classique (il voit l'objet se rapprocher de plus en plus lentement de l'horizon, et en reçoit des photons de plus en plus redshiftés, jusqu'à ne plus pouvoir les détecter; cf. le fil récent sur le dernier photon avant l'horizon).

Bref, la question pour laquelle j'ai commencé à faire dévier la discussion de son sujet n'avait pas lieu d'être - d'autant moins que l'origine de cette question était mon interprétation (certainement fausse) des figures du MTW représentant les géodésiques radiales en coordonnées de Schwarzschild... En fait la figure du cours de Gourgoulhon (pour les géodésiques lumière) est moins trompeuse. Mais la différence de représentation ne découle que du choix (arbitraire, comme mach3 nous l'a rappelé) du sens de la coordonnée t dans la région II : évidemment, si on choisit le même sens que dans la région I, on ne peut pas tracer les deux parties d'une même géodésique entrante, puisqu'il faudrait la prolonger au-delà de t = infini...
Donc je pense qu'on peut mettre un point final à cette partie de la discussion, à moins que tu aies de nouvelles questions en relation avec le sujet initial du fil.

PS pour mach3 : si tu scindes le fil et en ouvres un nouveau sur la croissance des TN, et qu'on continue à y discuter des "bonnes" solutions pour traiter cette question autrement qu'avec les mains, il aurait plutôt sa place dans la section "astrophysiciens" car ça va vite devenir très technique.
De mon côté je peux approfondir la question en utilisant la métrique LTB : j'ai déjà pondu pour mon propre usage un document en LaTEX dans lequel je détaille les calculs pour l'évolution de zones de sous- ou sur-densité, avec application numérique et courbes basées sur des hypothèses "réalistes" (amplitude des anisotropies du CMB et rayon du "sound horizon"). Les résultats n'ont pas l'air idiots : l'évolution jusqu'à l'époque actuelle produit des vides cosmiques et des amas de taille et de densité raisonnables (à ça près que, pour simplifier, j'ai plongé ces zones "LTB" dans un espace-temps d'EDS, sans constante cosmo). Donc je pense que ça tient à peu près la route - au moins jusque-là (je comptais me servir de ça comme base pour construire un toy-model réaliste de cosmo inhomogène; mais je n'avais pas réalisé que si je plongeais mes zones LTB dans un espace-temps EDS à tout t, le résultat serait évidemment un espace-temps moyen EDS à tout t. Bref, beaucoup de sueur dépensée pour rien.)
J'y avais fait l'hypothèse que les zones sur-denses en contraction se virialisaient assez tôt pour ne pas conduire à une singularité. Je peux reprendre les calculs en faisant sauter cette hypothèse et (pour l'application numérique) en prenant des hypothèses de départ (rayon et densité de la zone) compatibles avec la formation d'une galaxie isolée, pour aller jusqu'à l'apparition d'un horizon (du trou noir central de la future galaxie!) et essayer de voir comment cet horizon évolue ensuite (tant que la métrique LTB reste applicable à l'extérieur, donc avant virialisation et en supposant que la pression reste négligeable).
Mais j'aurai peut-être besoin de quelques encouragements pour m'y remettre... D'autant plus que je vais probablement réinventer l'eau chaude vu qu'il y a déjà un paquet de publications sur le sujet. Mais en général les publications ne donnent pas le détail des calculs et il n'y a qu'en m'y collant moi-même que j'arrive à bien cerner un problème.

[JPL]

PS pour mach3 : si tu scindes le fil et en ouvres un nouveau sur la croissance des TN, et qu'on continue à y discuter des "bonnes" solutions pour traiter cette question autrement qu'avec les mains, il aurait plutôt sa place dans la section "astrophysiciens" car ça va vite devenir très technique.

Oui à condition que n’importe qui ne s’autorise pas à y intervenir !

[Mailou75]

Re,

Et cela se produit au bout d'un intervalle de temps fini Δt₁ pour l'observateur, puisque ça ne demande pas que cette masse ait traversé l'horizon initial de rayon R. Autrement dit, pour l'observateur le nouvel horizon est moins loin dans le temps (puisque Δt₁<+∞).

L'horizon se rapproche spatialement puisqu'il grandit et qu'on suppose l'observateur fixe. Moins loin "dans le temps" je ne sais pas... le résultat est toujours un TN de Schw avec exactement les mêmes caractéristiques à part qu'il est plus grand. Dans le "doc" ils soudent des bords de jambes de pantalon notées I+ (cad l'infini du temps). Cette notion de "distance temporelle" surtout pour un observateur qui reste à distance est plus que floue, trop vite survolée dans le doc…

Il me semble qu'on s'est beaucoup éloigné du sujet initial de la discussion (le "travail du champ de gravitation en RG")... Cela vaudrait peut-être la peine de scinder ce fil, non ?

Vu les sujets que tu annonces il en faudrait deux : un sur la croissance des trous noirs et un sur la cosmo (avec les zones de sous densité). Tenter un lien direct, à froid, est un peu osé...

Mais ça n'avait déjà qu'un rapport assez indirect avec le sujet initial.

Non, complètement dans le sujet : les vitesses entre Vlib et c (= vitesse non nulle à l'infini)

J'ai rarement le courage de lire les entre Mailou et Zefram

Pour le coup on était trois, mach3 a beaucoup participé, c'est à lui qu'on doit dr/dt et dr/dT paramétrés par K (ou autre) et ce fil à la bonne idée de Zef de multiplier les gammas… alors que perso je n'étais pas du tout chaud.

A +

Mailou

[yves95210]

Oui à condition que n’importe qui ne s’autorise pas à y intervenir !

Tant que les interventions sont justifiées (ou qu'il s'agit de questions), je ne vois pas pourquoi ça poserait un problème.

Si ça s'adresse à Mailou et Zefram, je trouve ta remarque un peu déplacée. L'un et l'autre ont montré depuis longtemps qu'ils font des efforts pour apprendre (et pas se contenter de présentations vulgarisées des sujets), même si Mailou rame un peu avec les maths . A ce titre, en tant qu'"étudiants avancés", ils ont autant le droit que d'autres d'intervenir dans le sous-forum "astrophysiciens etc." (dont le nom n'a d'ailleurs pas suscité beaucoup de vocations depuis sa création).
Si l'un ou l'autre ont pu dire des bêtises à l'occasion, ils ne sont pas les seuls, j'en ai aussi écrit un paquet sur le forum Futura (et encore dans ce fil probablement). Et je suis autant autodidacte qu'eux sur ces sujets, avec (peut-être) l'avantage d'avoir fait autrefois des études en maths-physique un peu plus poussées.

Avant d'émettre un tel oukase (bon, c'était pas en vert, mais quand-même), tu aurais pu au moins demander l'avis de mach3, qui, en plus de son rôle de modérateur, est intervenu activement dans cette discussion ou dans d'autres avec les mêmes.

Quoi qu'il en soit, si on continue la discussion sur un sujet aussi technique, équations et documents à l'appui, je doute que ça attire beaucoup de monde...

[yves95210]

L'horizon se rapproche spatialement puisqu'il grandit et qu'on suppose l'observateur fixe. Moins loin "dans le temps" je ne sais pas... le résultat est toujours un TN de Schw avec exactement les mêmes caractéristiques à part qu'il est plus grand. Dans le "doc" ils soudent des bords de jambes de pantalon notées I+ (cad l'infini du temps). Cette notion de "distance temporelle" surtout pour un observateur qui reste à distance est plus que floue, trop vite survolée dans le doc…

On en reparlera quand j'aurai un peu avancé (pas tout seul j'espère) dans la recherche d'une solution plus réaliste que celle de Schwarzschild, autorisant le trou noir à grossir.
Mais dans mon explication "avec les mains", l'idée c'est que, plus vite la masse s'accumule autour de l'horizon, plus vite celui-ci grandit - ce qui, de fait, le "rapproche" temporellement du présent d'un observateur pour qui il était initialement dans l'infini futur.

Vu les sujets que tu annonces il en faudrait deux : un sur la croissance des trous noirs et un sur la cosmo (avec les zones de sous densité). Tenter un lien direct, à froid, est un peu osé...

Je ne parlais pas de faire un lien avec la cosmo, je citais juste un travail perso que j'avais commencé effectivement dans le but d'élaborer un "toy model" cosmologique, mais dont je ne parle d'utiliser qu'une partie, en l'adaptant au cas de l'effondrement gravitationnel qui donne lieu à la naissance d'une galaxie, avec son trou noir central. Pour ça la métrique LTB est l'outil adapté, tant qu'on se contente d'une solution à symétrie sphérique et qu'on peut considérer qu'on a affaire à un fluide parfait, sans pression. Et ça a l'avantage de ne pas être trop compliqué pour mes compétences limitées.
Cela ne sera pas représentatif de tous les types de trous noirs qu'on peut rencontrer dans l'univers, mais ça permettra peut-être quand-même de se faire une idée plus réaliste de la manière dont les TN grossissent, dans un espace-temps qui n'est pas aussi vide que celui de Schwarzschild...

Non, complètement dans le sujet : les vitesses entre Vlib et c (= vitesse non nulle à l'infini)

Oui, j'ai parcouru vite fait votre discussion, compris la démarche et corrigé mon premier message.

Pour le coup on était trois, mach3 a beaucoup participé, c'est à lui qu'on doit dr/dt et dr/dT paramétrés par K (ou autre) et ce fil à la bonne idée de Zef de multiplier les gammas… alors que perso je n'étais pas du tout chaud.

Oui, j'ai vu. Mais parmi les smileys je n'en ai pas trouvé qui représente une discussion (animée) à trois .
Et je trouvais que celui-ci résumait bien vos échanges habituels, à Zefram et à toi, que pas grand-monde n'a le courage de suivre à part mach3, respect à lui

[JPL]

Tant que les interventions sont justifiées (ou qu'il s'agit de questions), je ne vois pas pourquoi ça poserait un problème.

Si ça s'adresse à Mailou et Zefram, je trouve ta remarque un peu déplacée. L'un et l'autre ont montré depuis longtemps qu'ils font des efforts pour apprendre (et pas se contenter de présentations vulgarisées des sujets), même si Mailou rame un peu avec les maths . A ce titre, en tant qu'"étudiants avancés", ils ont autant le droit que d'autres d'intervenir dans le sous-forum "astrophysiciens etc." (dont le nom n'a d'ailleurs pas suscité beaucoup de vocations depuis sa création).

Chacun le prend comme il veut et nous n’espérions pas que cela suscite une ruée dans les mois suivant sa création. Mais il faut être conscients que le forum d’astrophysique où tout était mélangé était devenu la honte de Futura vu par les professionnels. Au moins la séparation en trois rend les choses claires et la porte reste ouverte pour des contributions de qualité. C’est un investissement sur le long terme.

[JPL]

Je précise qu’il y a des interventions de qualité actuellement et des efforts méritants, même s’ils sont encore incertains de la part de certains.